![]() 傪桳棟悢偲偡傞偲偒丄
傪桳棟悢偲偡傞偲偒丄
曽掱幃
![]() 丂丂丂丂丂丂俙
丂丂丂丂丂丂俙
偼帺慠悢夝傪傕偮偐丅
摿掕偺忦審偺偲偒丄帺慠悢夝傪傕偨側偄偙偲偼徹柧偝傟偰偄傞丅摿掕偺忦審偲偼丄
値亞俁偱丄![]() 偺偲偒偱丄
偺偲偒偱丄
![]()
偱偁傞丅偡側傢偪丄桳柤側僼僃儖儅乕偺掕棟偱偁傞丅
丂幃俙偼忢偵帺慠悢夝傪傕偨側偄偩傠偆偐丅値亖俀偺偲偒偼丄
![]()
偵偍偄偰丄倎傑偨偼們偑暯曽悢側傜偽丄帺慠悢夝偑柍尷偵懚嵼偡傞偙偲偼丄偡偱偵偙偺俫俹忋偱徹柧偝傟偰偄傞丅
丂値亞俁偺偲偒偼偳偆偱偁傠偆偐丅師偺応崌丄帺慠悢夝偑柍尷偵懚嵼偡傞偙偲偼帺柧偱偁傞丅倎丆倐傪帺慠悢偲偟丄
![]()
![]()
![]()
偲側傞偲偒偱偁傞丅偙偺応崌丄幃俙偼師偺傛偆偵場悢暘夝偝傟傞丅
![]()
傛偭偰丄乮倶丆倷丆倎倶亄倐倷乯偼幃俙偺帺慠悢夝偱偁傞丅倶丆倷偼擟堄偺帺慠悢傪偲傞偙偲偑偱偒傞偺偱丄幃俙偺帺慠悢夝偼柍尷偵懚嵼偡傞丅
丂偙傟偐傜偺尋媶壽戣偼丄偄偐側傞偲偒偵幃俙偼柍尷偵帺慠悢夝傪傕偮偺偐丄傑偨偼傕偨側偄偺偐偱偁傞丅
丂側偍丄幃A偑惍悢夝傪傕偮偲偄偆偙偲偲桳棟悢夝傪傕偮偙偲偼摨抣偱偁傞丅側偤側傜桳棟悢夝![]() 偑懚嵼偟偨偲偡傞偲丄
偑懚嵼偟偨偲偡傞偲丄![]() 偺暘曣偺岞攞悢倣偵傛偭偰丄
偺暘曣偺岞攞悢倣偵傛偭偰丄![]() 偼惍悢偺慻偱偁傞偑丄
偼惍悢偺慻偱偁傞偑丄![]() 偺偲偒丄
偺偲偒丄
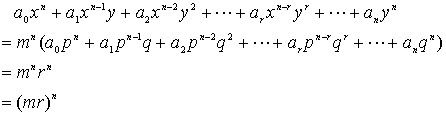
偺寁嶼偐傜![]() 傕幃A偺夝偱偁傞偐傜偱偁傞丅
傕幃A偺夝偱偁傞偐傜偱偁傞丅
丂摨條偵![]() 偑桳棟悢夝偺偲偒丄擟堄偺桳棟悢兛傪偐偗偨
偑桳棟悢夝偺偲偒丄擟堄偺桳棟悢兛傪偐偗偨![]() 傕幃俙偺夝偱偁傞丅偙傟傜傪暿偺夝偲偡傞偲丄夝偼懚嵼偡傞偲偡傟偽忢偵柍尷偵偁傞偙偲偵側偭偰偟傑偆偺偱丄偙偙偱偼
傕幃俙偺夝偱偁傞丅偙傟傜傪暿偺夝偲偡傞偲丄夝偼懚嵼偡傞偲偡傟偽忢偵柍尷偵偁傞偙偲偵側偭偰偟傑偆偺偱丄偙偙偱偼![]() 偺偲偒丄夝
偺偲偒丄夝![]() 偲夝
偲夝![]() 傪摨堦夝偲掕媊偡傞偙偲偵偡傞丅偟偨偑偭偰丄堎側傞夝偺掕媊偼丄
傪摨堦夝偲掕媊偡傞偙偲偵偡傞丅偟偨偑偭偰丄堎側傞夝偺掕媊偼丄![]() 偲側傞偙偲偱偁傞丅
偲側傞偙偲偱偁傞丅
奼戝僼僃儖儅乕梊憐
曽掱幃
![]()
偼値亖俀偺応崌傪娷傔偁傞忦審壓偱偼帺慠悢夝傪堦偮傕帩偨側偄丅
