第19講 特殊種による魔方陣ソフトの高速化
第6話 特殊種を合成留際の注意点
3話に渡って特殊種作成ソフトの解説をしてきました。
では、いよいよ2つの種を組み合わせて魔方陣を合成したいと思います。
任意の2つを組み合わせて魔方陣は合成できるでしょうか。
特殊種作成ソフトをビルドしてTextBoxに5を入力して実行ボタンを押すと、
ソフトが作る最初の2つは、
|
0 |
1 |
2 |
3 |
4 |
| 0 |
□4□ |
□1□ |
□3□ |
□2□ |
□0□ |
| 1 |
2 |
0 |
1 |
3 |
4 |
| 2 |
0 |
3 |
2 |
4 |
1 |
| 3 |
3 |
4 |
0 |
1 |
2 |
| 4 |
1 |
2 |
4 |
0 |
3 |
|
0 |
1 |
2 |
3 |
4 |
| 0 |
□4□ |
□3□ |
□1□ |
□2□ |
□0□ |
| 1 |
2 |
0 |
4 |
3 |
1 |
| 2 |
3 |
1 |
2 |
0 |
4 |
| 3 |
0 |
4 |
3 |
1 |
2 |
| 4 |
1 |
2 |
0 |
4 |
3 |
ですが、次の規則で合成します。一つ目の種の各セルに5を書け、2つ目の種の同じ位置のセルを加え、さらに1加えます。
すると、
|
0 |
1 |
2 |
3 |
4 |
| 0 |
25 |
9 |
17 |
13 |
1 |
| 1 |
13 |
1 |
10 |
19 |
22 |
| 2 |
4 |
17 |
13 |
21 |
10 |
| 3 |
16 |
25 |
4 |
7 |
13 |
| 4 |
7 |
13 |
21 |
5 |
19 |
となります。
確かに対角線合計、逆対角線合計、
すべての列合計、すべての行合計
がすべて65になります。
ですが、左表は魔方陣と言えるでしょうか。
よく見れば問題はお分かりですね。
|
0 |
1 |
2 |
3 |
4 |
| 0 |
25 |
9 |
17 |
13 |
1 |
| 1 |
13 |
1 |
10 |
19 |
22 |
| 2 |
4 |
17 |
13 |
21 |
10 |
| 3 |
16 |
25 |
4 |
7 |
13 |
| 4 |
7 |
13 |
21 |
5 |
19 |
そうです。
同じ色の数字が重複してしまっているのです。
これは、魔方陣には1から25までの数字をもれなく重複なく
入れなければならないという原則に反しています。
実は、2つの魔方陣を結婚させるには、
厳しい条件が必要なのです。
相性の悪い二人を結婚させると、
左のようなできの悪い子供(疑似魔方陣)ができてしまうのです。
魔方陣もどきができないような2つの種のよい相性とは何でしょうか、
どのようなときに2つはめでたく結婚が許されるのでしょうか。
答えは、2つの種が直交するということです。
直交の例は皆さんがすでにご存じです。
| □0□ |
□1□ |
□2□ |
□3□ |
□4□ |
| 3 |
4 |
0 |
1 |
2 |
| 1 |
2 |
3 |
4 |
0 |
| 4 |
0 |
1 |
2 |
3 |
| 2 |
3 |
4 |
0 |
1 |
| □0□ |
□1□ |
□2□ |
□3□ |
□4□ |
| 2 |
3 |
4 |
0 |
1 |
| 4 |
0 |
1 |
2 |
3 |
| 1 |
2 |
3 |
4 |
0 |
| 3 |
4 |
0 |
1 |
2 |
直交とは何でしょうか。それは、第1の種をx座標、第2の種をy座標として組み合わせたときに、
(0,0),(1,1),(2,2),(3,3),(4,4),(3,2),(4,3),(0,4),(1,0),(2,1),(1,4),
(2,0),(3,1),(4,2),(0,3),(4,1),(0,2),(1,3),(2,4),(3,0),(2,3),(3,4),
(4,0),(0,1),(1,2)の各点に重複がないことです。
つまり、直線x=0、y=0、x=4、y=4で囲まれた正方形の各格子点が漏れなくすべて揃うことです。
もっとわかりやすくいえば、各座標に碁石をおいていったときに碁石の重複がなく、25個がすべてがおける状態です。
残念ながら、今回作成したソフトで作った特殊種1000個の中には直交する組み合わせは存在しません。
おそらく、10万個作らせたとしても1つも直交しないでしょう。
そこで、ソフトを次のように改良することによって4次以上の魔方陣が作成できるようにします。
#pragma once
#include<stdlib.h>
int n;
int a1[10][10],a2[10][10],p[10][10];
int x[100],y[100];
int s;
namespace 魔方陣特殊種作成ソフト {
・
・
・
#pragma endregion
private: System::Void button1_Click(System::Object^
sender, System::EventArgs^ e) {
if(s==1000)return;
int i,j,k,h,wa,kk,kkk,m;
・
・
・
int i,j;
for(i=0;i<n;i++){
for(j=0;j<n;j++){
p[i][j]=0;
}
}
f1(0);
・
・
・
w[9]=L"魔";w[10]=L"方";w[11]=L"陣";w[12]=L"総";w[13]=L"数";w[14]=L":";w[15]=s.ToString();
・
・
・
}
void g1(char n){
・
・
・
}
void g2(char n){
・
・
・
}
void f1(char g){
if(s==1000)return;
int i,j,k,h,wa,kk,kkk,m;
(array<String^>^ w=gcnew array<String^>(16);を削る。)
rand();
rand();
kk=rand()%n;
・
・
・
a1[y[g]][x[g]]=kkk; (以下aはすべてa1に変更)
・
・
・
if(h==1){
if(g<n*n-1){
f1(g+1);
}
else{
f2(0);
if(s==1000)return;
}
}
}
}
void f2(char g){
if(s==1000)return;
int i,j,k,h,wa,kk,kkk,m,xx,yy,,hh;
yy=a1[y[g]][x[g]];
・
・
・
a2[y[g]][x[g]]=kkk;
h=1;
hh=0;
xx=a2[y[g]][x[g]];
(ここに、直交してなければh=1になるようなソースを入れる)
if(h==1){
・
・
・
if(h==1){
if(g<n*n-1){
f2(g+1);
}
else{
・
・
・
s++;
if(s==1000)return;
}
}
}
if(hh==1)p[yy][xx]=0;
}
};
}
ピンクは変更点、赤は追加です。
f2も特殊種を作らせる関数ですから、
f2はほとんどf1と仕組みが同じです。
違う点は、f1で作った種と直交するような種を作るように工夫しなければならない点(直交してなければh=1)です。
また、
・
・
・
の部分は2つの種を合成して、魔方陣を作らせる部分です。
皆さん、考えてみてください。
今までの課題で一番の難問と言えます。
頑張ってください。
ヒントは、新しいグローバル配列p[10][10]を用意していることです。
また、yy=a1[y[g]][x[g]];、xx=a2[y[g]][x[g]];、hh=0;;、if(hh==1)p[yy][xx]=0;の意味も考えてみてください。
新たに用意した配列はp[yy][xx]として使用します。
また、特殊種法では6次魔方陣はできませんので、デザインの方も
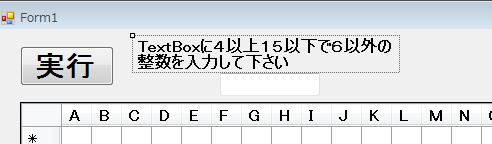
と変更しておきましょう。
第19講第5話へ 第19講第7話へ

VC++講義第1部へ
vb講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual
Basic入門基礎講座

