この講の主題である関数の再帰的呼び出しによる方法だと、
どのようなソースになるかお見せしましょう。
#pragma once
int n=3;
int a[3];
int s;
・
・
・
#pragma endregion
String^ w;
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
w=L"";
s=0;
f(0);
w+=L"\n"+L"順列総数:"+s.ToString();
label1->Text=w;
}
void f(char g){
int i,j,k,h;
for(i=0;i<n;i++){
a[g]=i+1;
h=1;
if(g>0){
for(j=0;j<g;j++){
if(a[g]==a[j]){
h=0;
break;
}
}
}
if(h==1){
if(g<n-1){
f(g+1);
}
else{
for(k=0;k<n;k++)w+=a[k].ToString()+L" ";
w+=L"\n";
s++;
}
}
}
}
関数の再帰的呼び出しといわれる所以は、f(g+1);にあります。
関数の中で自分自身を呼び出しています。
このプログラムソースは、初心者の方にとってはもちろんのこと、
ある程度プログラムの勉強をされた方にとっても、
理解できない,というところが正直なところではないでしょうか。
むしろ、第1話のfor文のソースより難解であるといってよいと思います。
ですから、このソースの解説については、
3話か4話に渡ってかなり時間をかけて解説していきます。
ですが、ここでの注目点だけ説明しておきましょう。
このプログラムは、1,2,3の3つの順列を作成するようになっていますが、
int n=3;の3を例えば7に変更するだけで、
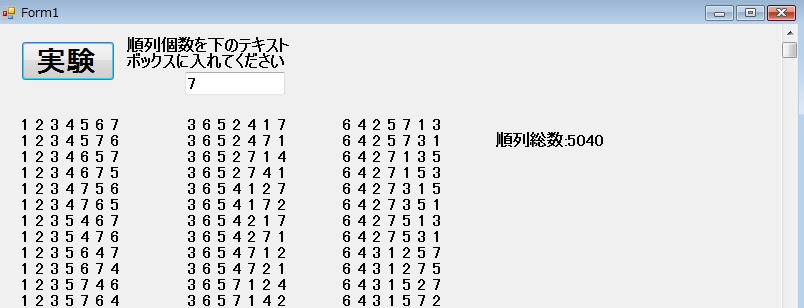
1,2,3,4,5,6,7の7つの順列を作成するように変更することができます。
さらに、Form1に次のようにテキストボックスを入れておいて、

そこから、nの値を取得するようにしておけば、
何個の順列でも作成可能な普遍的(広範囲)なプログラムに変身します。
#pragma once
int n;
int a[7];
int s=0;
・
・
・
#pragma endregion
String^ w1;
String^ w2;
String^ w3;
String^ w4;
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
w1=L""; w2=L""; w3=L""; w4=L"";
n=int::Parse(textBox1->Text);
f(0);
w4+=L"\n"+L"順列総数:"+s.ToString();
label1->Text=w1;
label3->Text=w2;
label4->Text=w3;
label5->Text=w4;
}
void f(char g){
int i,j,k,h;
for(i=0;i<n;i++){
a[g]=i+1;
h=1;
if(g>0){
for(j=0;j<g;j++){
if(a[g]==a[j]){
h=0;
break;
}
}
}
if(h==1){
if(g<n-1){
f(g+1);
}
else{
if(s<2000){
for(k=0;k<n;k++)w1+=a[k].ToString()+L" ";
w1+=L"\n";
}
if(s<4000 && s>=2000){
for(k=0;k<n;k++)w2+=a[k].ToString()+L" ";
w2+=L"\n";
}
if(s<6000 && s>=4000){
for(k=0;k<n;k++)w3+=a[k].ToString()+L" ";
w3+=L"\n";
}
if(s<8000 && s>=6000){
for(k=0;k<n;k++)w4+=a[k].ToString()+L" ";
w4+=L"\n";
}
s++;
}
}
}
}
labelを増やした理由は、labelで表示できる行数に限りがあるからです。
実験では3000行は表示できないようなので、各labelで2000行表示させるようにしてあります。
尚、Form1のプロパティのAutoScrollはTrueにしておいて下さい。
スクロールできるようにしておかないとすべての表示ができないからです。
2000行ずつで4つのlabelを用意しましたが、
これでも7個の順列(総数は7!=5040個)が限界です。
この問題を解決するため後にlabelではなく、DataGridViewを利用する方法を紹介します。
DataGridViewなら何万行でも表示可能です。
それに対して、for文の方はソースを書く気力が失せるほど大変です。
今回は、Visual C++で書く気力が起きませんので、
VB講義から同様なプログラムソースを引用させて頂きます。
以下のソースは、初心者の方(プログラミングの経験が全くない方を想定しています。)にとっては、見たことがないVisual Basicによるソースです。
ですから、大変さだけ感じ取って頂ければよいと思います。
ですが、言語が違っても雰囲気は似ているのはお分かりになると思います。
Visual C++をここまで勉強されてきた皆さんは、もちろん、なんとなくですがお分かりになるのではないでしょうか。
Private Sub CommandButton1_Click()
Dim i As Integer, j As Integer, k As Integer, l As Integer, h1 As Integer, h2 As Integer, h3 As Integer, h4 As Integer, h5 As Integer, h6 As Integer, jyn(7) As Integer
Dim sousuu As Long
sousuu = 0
For i = 1 To 7
jyn(1) = i
For j = 1 To 7
jyn(2) = j
h1 = 1
For k = 1 To 1
If jyn(2) = jyn(k) Then
h1 = 0
Exit For
End If
Next
If h1 = 1 Then
For k = 1 To 7
jyn(3) = k
h2 = 1
For l = 1 To 2
If jyn(3) = jyn(l) Then
h2 = 0
Exit For
End If
Next
If h2 = 1 Then
For l = 1 To 7
jyn(4) = l
h3 = 1
For m = 1 To 3
If jyn(4) = jyn(m) Then
h3 = 0
Exit For
End If
Next
If h3 = 1 Then
For m = 1 To 7
jyn(5) = m
h4 = 1
For n = 1 To 4
If jyn(5) = jyn(n) Then
h4 = 0
Exit For
End If
Next
If h4 = 1 Then
For n = 1 To 7
jyn(6) = n
h5 = 1
For o = 1 To 5
If jyn(6) = jyn(o) Then
h5 = 0
Exit For
End If
Next
If h5 = 1 Then
For o = 1 To 7
jyn(7) = o
h6 = 1
For p = 1 To 6
If jyn(7) = jyn(p) Then
h6 = 0
Exit For
End If
Next
If h6 = 1 Then
sousuua = sousuu Mod 8
sousuus = Int(sousuu / 8)
sousuu = sousuu + 1
For p = 1 To 7
Cells(5 + sousuus * 2, 1 + p + sousuua * 8) = jyn(p)
Next
End If
Next
End If
Next
End If
Next
End If
Next
End If
Next
End If
Next
Next
End Sub
7個の順列ですでにこんなに大変です。
これが10個、20個になるととても手に負えません。
それに対して、関数の再帰的呼び出しの方は、
表示の限界の問題さえ解決すれば、3次の順列のプログラムを少し改良するだけで、
普遍的なプログラムに変身します。
for文の場合、7次元ループぐらいが限界ですが、
関数の再帰的呼び出しの方は、理論的には無限次元のループが可能になります。
後で、何回も予告しておいた通り、数独問題作成ソフトの開発に挑戦しますが、
数独問題作成ソフトにおいては、
81×4=328次元ループになっています。
さらに、魔方陣作成にも挑戦しますが、200次魔方陣当たりでは20万次ループを軽く越えます。
このような多次元ループを実現しているものこそが、関数の再帰的呼び出しなのです。
