方程式![]() は自然数解を一つももたないことの証明
は自然数解を一つももたないことの証明
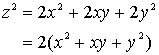
自然数解をもつと仮定する。
①
x,y両方を奇数であるとすると、![]() は奇数である。よって、
は奇数である。よって、![]() は無理数となって矛盾する。
は無理数となって矛盾する。
②
一方を奇数、他方を偶数であるとすると、![]() は奇数となり、
は奇数となり、![]() は無理数となって矛盾する。
は無理数となって矛盾する。
③
両方偶数であるとすると、x,yの最大公約数bによって![]() とおける。このとき、
とおける。このとき、![]() となり
となり![]() は無理数となって矛盾する。
は無理数となって矛盾する。
①②③より![]() は自然数解をもたない。
は自然数解をもたない。
さらに![]() より、
より、![]() も自然数解をもたない。
も自然数解をもたない。
方程式![]() は自然数解を一つももたないことの証明
は自然数解を一つももたないことの証明
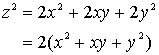
自然数解をもつと仮定する。
①
x,y両方を奇数であるとすると、![]() は奇数である。よって、
は奇数である。よって、![]() は無理数となって矛盾する。
は無理数となって矛盾する。
②
一方を奇数、他方を偶数であるとすると、![]() は奇数となり、
は奇数となり、![]() は無理数となって矛盾する。
は無理数となって矛盾する。
③
両方偶数であるとすると、x,yの最大公約数bによって![]() とおける。このとき、
とおける。このとき、![]() となり
となり![]() は無理数となって矛盾する。
は無理数となって矛盾する。
①②③より![]() は自然数解をもたない。
は自然数解をもたない。
さらに![]() より、
より、![]() も自然数解をもたない。
も自然数解をもたない。