第１話 全セルリスト構造解析
前回ヒント数を22にしましたが、
ヒント数が少ないので複数解を持つ可能性があります。
そこで
赤枠のところを
const int hnt = 0;
srand(2);
と変更してF5を押すと、
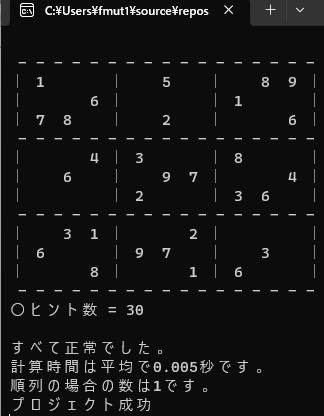
となっているはずです。
これが唯一解を持てば、数独ができたことになります。
ただし、今は理詰めで解くのではなく試行錯誤法で解きます。
試行錯誤法で解くと言っても、なにも工夫しないで解くわけではありません。
これを写しとったものがエクセルファイルです。
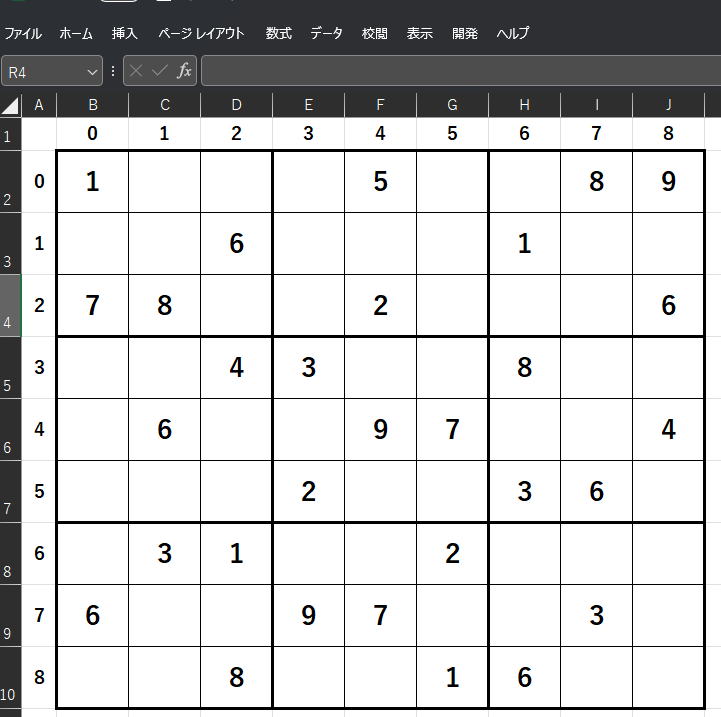
エクセルファイルをクリックして適当なフォルダに保存してください。
数独が得意な方は実際に解いてみてください。
理詰めで解けます。
前回
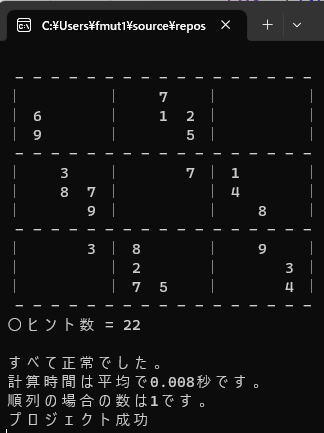第３講第１１話で
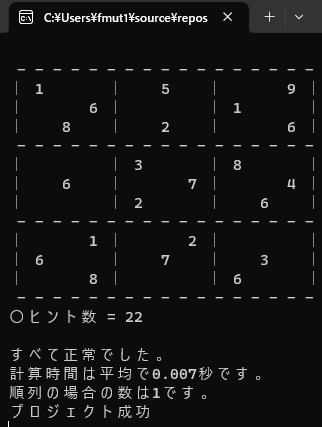に変更した理由は左だとヒント数を30までにしても別解が存在してしまっていたからです。
は唯一解になっており、しかも理詰めで解ける問題になっています。
理詰めで解ける問題というのは、空欄の中にただ一つの数字に決まる欄があるということです。
そして、その数字を埋めたことによって残りの空欄のなかに１つの数字に決まる欄が存在するのです。
唯一の数字に決まっているので仮定法を必要としないわけです。
皆さんも
をいくつまで減らしても唯一解になるか調べてください。実はヒント数29では理詰めで解けないようですから、
30にしてくださいと全く適当に言った数字がドンピシャリだったのです。
まあ、たまたまですが。
この図を
もとに説明していきます。まず、最初にやるべきことは私が全セルリスト構造解析と呼ぶ作業をすることです。
そして、次にやることは候補数字が少ない順にランキングすることです。
全セルリスト構造解析は全体構造解析とも呼称します。
空欄に数字を入れる度に全体リスト構造も変わるわけですが、
影響を受ける場所は同じ行・同じ列・同じブロックのみですから、
影響受けるセルのリスト構造解析をやればよいわけです。
影響を受けるセルのリスト構造解析を部分構造解析とします。
さて、全セルリスト構造解析の
水色付きのエクセルファイル全とは水色のすべてのセルを指します。
全セルリスト構造解析は、51個のセルについてリスト構造解析を行うということです。
それではリスト構造解析とは何でしょうか。
座標（0，1）に入る数字の候補を考えることが、
座標（0，1）のリスト構造解析になります。
まず、行の条件から1，5，8，9が候補から外されます。
次に、
列の条件から8（これは行の条件から外されています），6，3が候補から外されます。最後にブロック
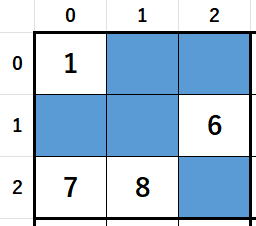の条件から1（すでに外さています），6（すでに外さています），7，8（すでに外さています）が候補から外れます。
以上から座標（0，1）に入る数字の候補は｛2，4｝となります。
これならわざわざリスト構造解析とは言わずに、
リストで充分だろうと皆さんはお考えになると思いますが、
｛2｜2，4｝という構造を持っているということで、
リスト構造解析などという難しい名前をつけました。
最初の2は候補数字の種類数です。
候補になる数字が2，4と2個あるという意味です。
メンバーも大事ですが、候補数字数（候補数）がいつくなのかも決定的に重要な情報です。
｛2，4｝の中にその情報は含まれているので、
｛2｜2，4｝とする必要はないだろう、
というご意見はごもっともです。
ですが、候補を明らかにするとともに候補数も明らかにする必要があります。
理由はif文やfor文で処理を行うからです。
そうは言っても｛2，4｝がわかれば候補数がわかるので、
単にリスト解析の方がよいと思う方はそれで通してください。
私は、魔方陣自動生成に取り組んでいた時からリスト構造解析と呼んできましたので、
数独でもリスト構造解析と呼びます。
では、リスト構造解析ないしはリスト解析は、具体的にはどうしたらよいのでしょうか。
まず、色のある座標（0，1）を
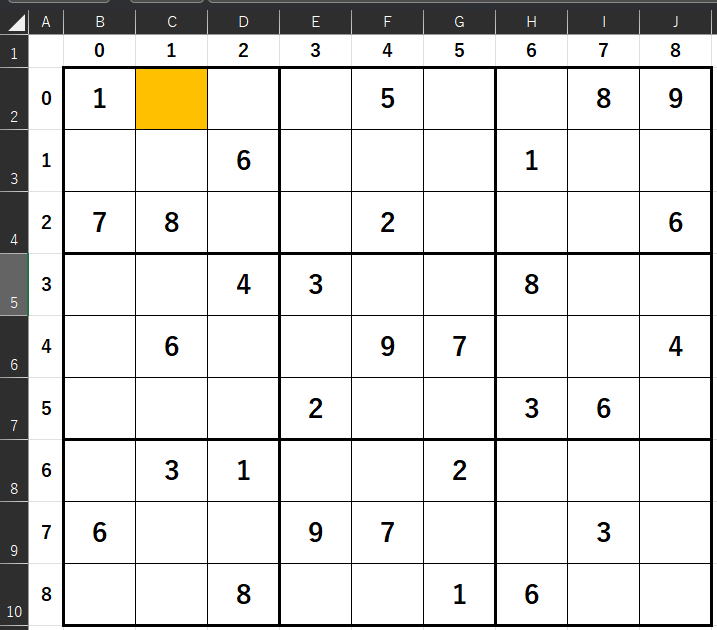
for文とif文を組み合わせてリスト構造解析をやってみましょう。
将来空欄になっている場所に候補数字の個数が小さい順部屋番号を割り振って
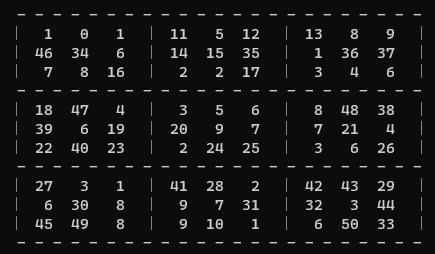
としますので、
と変更してください。
ノーヒントでは難しいと思いますので、第２話で考え方を説明して第３話で答え合わせをします。
第３講第11話へ 第２話へ
トップへ