第11話 ヒントの数字を置く場所以外は空欄にする
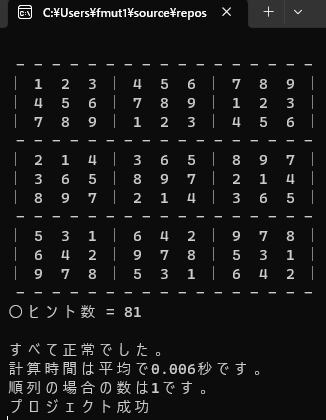 から
から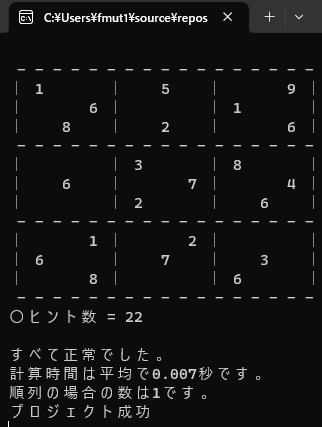 へ
へを実現するプロジェクト例
#include<iostream>
#include<conio.h> //while (!_kbhit()); を使うためのお呪い。
using namespace std;
void f(int s); //sは次元番号=部屋番号
const int n = 9; //16次数独や25次数独も考えてnと一般化した。
int cn = 0; //順列を数える変数
int m[n][n]; //解答用2次元配列(魔方陣の研究から始まったので本体をmとしてきた。
int mon[n][n]; //m[n][n]は解答用なので、問題用の2次元配列を用意した。
int sng = 1;//1ならば真
const int hnt = 22;
int main() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
mon[i][j] = 0; //解答用であるm[n][n]は後に(ヒント数0の数独を解くときに)必ず値が埋まるが、
//問題用の場合その保証がない。
}
}
clock_t hj, ow;
hj = clock();
f(0);
cout << "ヒント数 = " << hnt << endl;
ow = clock();
if (sng == 1)cout << endl << "すべて正常でした。" << endl;
cout << "計算時間は平均で" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl;
cout << "順列の場合の数は" << cn << "です。" << endl;
cout << "プロジェクト成功" << endl;
while (!_kbhit()); //待機させるための命令
return(0);
}
void f(int s) {
int y = s / 9; //縦座標
int x = s % 9; //横座標
unsigned u = (unsigned)time(NULL);
srand(2); //シード値を現在の時刻から取得
//本来はsrand(u);だがこれだと毎回異なったものになり
//私の実行画面と読者の実行画面が同じにならないので一時的にsrand(2); としている
int ii = rand() % 9; //始まりをランダムにする
for (int i = 0; i < n; i++) {
m[y][x] = (i + ii) % n + 1; //2次元配列に1から9までの整数を入力
if (x > 0) {
for (int j = 0; j < x; j++) {
if (m[y][x] == m[y][j])goto tobi; //行の重複を防ぐ
}
}
if (y > 0) {
for (int j = 0; j < y; j++) {
if (m[j][x] == m[y][x])goto tobi; //行の重複を防ぐ
}
}
if (y % 3 == 1) {
for (int j = 0; j < 3; j++) {
if ((x / 3) * 3 + j != x) {
if (m[y][x] == m[y - 1][(x / 3) * 3 + j])goto tobi; //ブロックの重複を防ぐ
}
}
}
if (y % 3 == 2) {
for (int j = 0; j < 3; j++) {
if ((x / 3) * 3 + j != x) {
if (m[y][x] == m[y - 2][(x / 3) * 3 + j])goto tobi; //ブロックの重複を防ぐ
if (m[y][x] == m[y - 1][(x / 3) * 3 + j])goto tobi; //ブロックの重複を防ぐ
}
}
}
if (s + 1 < n * n)f(s + 1); //1つ奥の部屋に入室
if (cn == 1)return; //数独が1個できた時点で止める
if (sng == 0)return; //異常があった時点でプロジェクトを止める
if (s == n * n - 1) { //一番奥に部屋に到達
int hb; //部屋番号
int tbs[6] = { 11,13,17,19,23,29 }; //飛びの選択肢 素数であれば81と互いに素は保証されている
int st = rand() % 81; //始めの位置
int tb = tbs[rand() % 6]; //飛び
int h = 0; //可否の否
cout << endl;
for (int j = 0; j < 17; j++)cout << " -"; //最初の横線
cout << endl;
int* gohr = (int*)calloc(hnt, sizeof(int));
for (int t = 0; t < hnt; t++) {
gohr[t] = (st + t * tb) % 81;
}
for (int j = 0; j < n; j++) {
cout << "|";//縦線
for (int k = 0; k < n; k++) {
int hb; //部屋番号
hb = n * j + k; //初期化
int h = 0; //可否の否
for (int t = 0; t < hnt; t++) {
if (gohr[t] == hb) {
h = 1;
break;
}
}
if (h == 1) {
cout << " " << m[j][k] << " "; //2次元配列を2次元に並べる
mon[j][k] = m[j][k]; //問題用の配列に代入
}
else {
cout << " " << " " << " "; //空欄を作る
}
if (k % 3 == 2)cout << "|";//縦線
}
if (j % 3 == 2) {
cout << endl;
for (int k = 0; k < 17; k++)cout << " -"; //横線
}
cout << endl;
}
free(gohr); //メモリ解放
int p[9];//重複検査のための配列
int kr;
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++)p[k] = 0;//初期化
kr = 1; //初期化
for (int k = 0; k < n; k++) {
p[m[j][k] - 1] = 1;
}
for (int k = 0; k < n; k++) {
if (p[k] == 0) { //行の重複検査
cout << "×";
kr = 0;
sng = 0;
goto tobi1;
}
}
for (int k = 0; k < n; k++)p[k] = 0;//初期化
kr = 1; //初期化
for (int k = 0; k < n; k++) {
p[m[k][j] - 1] = 1;
}
for (int k = 0; k < n; k++) {
if (p[k] == 0) { //列の重複検査
cout << "×";
kr = 0;
sng = 0;
goto tobi1;
}
}
for (int k = 0; k < n; k++)p[k] = 0;//初期化
kr = 1; //初期化
for (int k = 0; k < n; k++) {
p[m[3 * (j / 3) + (k / 3)][3 * (j % 3) + (k % 3)] - 1] = 1;
}
for (int k = 0; k < n; k++) {
if (p[k] == 0) {
cout << "×";
kr = 0;
sng = 0;
goto tobi1;
}
}
}
tobi1:;
if (kr == 1)cout << "〇";
cn++;
if (cn == 1)return; //数独が1個できた時点でとめる
}
tobi:;
}
}
ヒントの数字が置いてある数独(本来の数独)を解くことが次の課題です。
これは実に大変困難な課題です。
その課題に取り組んでいく過程でヒント数0の数独を解くの高速化アイデアが生まれます。
 そのアイデアを生かせば0.008秒はもっと短い時間に代わります。
そのアイデアを生かせば0.008秒はもっと短い時間に代わります。二桁以上変わることを予言しておきましょう。
第10話へ 第4講第1話へ
トップへ