第２話 リスト構造解析をするためのヒント
ノーヒントでは難しいと思いますので、少しだけ考え方を説明したいと思います。
まず、変数名の変更について説明します。
int sudoku[n][n]; //解答用２次元配列（魔方陣の研究から始まったので本体をmとしてきた。
int mondai[n][n]; //sudoku[n][n]は解答用なので、問題用の２次元配列を用意した。
int sng = 1;//１ならば真
const int hnt = 30;
void cellslstkaiseki();
int lst[9][9][9];//セルリスト構造解析によって可能な数字を収容する３次元配列
int mx[9][9];//セルの数字候補の個数
sudokuは前はmとしていましたが、
それではセルの数字候補の個数を表すint mx[9][9];と混同してしまう可能性がありますので、
上のように変更しました。
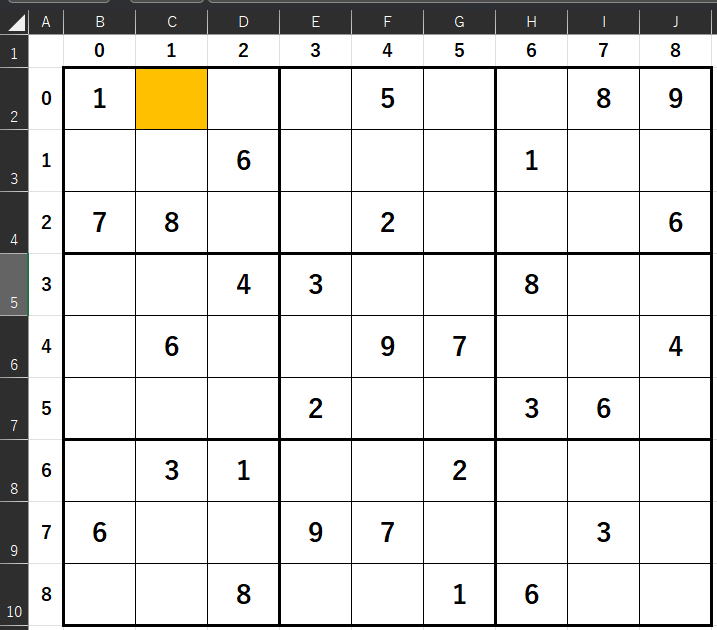
座標(0,1）のリスト構造解析は、最初は
for (int i = 0; i < n; i++)lst[0][1][i] = i + 1;//初期化 1から9までをリスト
1から9までの数字を入力します。
すべて空欄の時は、外される数字がないのでこのようにします。
この場合{1,2,3,4,5,6,7,8,9}のすべてが候補の数字なので、
mx[0][1] = 9;//候補数字いったん0に初期化しておく
とした方がよいと思うでしょうが、
mx[0][1] = 0;//候補数字いったん0に初期化しておく
いったん0に初期化します。理由はあとで数え直すからです。
さて、重複する候補数字を外すのに３段階を踏みます。
まず、行の重複
を調べるために
セルを緑のように動かしていって、0より大きい数が入っている場合その数字を外さなければなりません。
すなわち、重複対象をさがすために(0,0)から初めて(0,8)まで動かしていって重複するものはリストから外すわけです。
注意事項はオレンジのセルすなわちセルリスト解析をしているmondai[0][1]は
飛ばすようにしなければなりません。
ここに重要な秘密が隠されています。
セルの(0,8)を本質（条件）を規定するのは、自分自身にはなく自分の外部にあるのです。
人間の本質は自分自身の中にはなくて、他との諸関係にあるのです。
「人間の本質は社会的諸関係の総体である」（カール・マルクス）
重要な秘密とは、初心者はセルの内側（リスト=候補数字）にのみに注目しますが、
本当はセルの外側を見るべきだということです。
外側を見た時に、初めて理詰めで解けるのです。
さて、重複対象は
(0,0),(0,4),(0,7),(0,8)です。
すなわち。1，5，8，9です。
外すために0にします。
{0,2,3,4,0,6,7,0,0}
次は、列
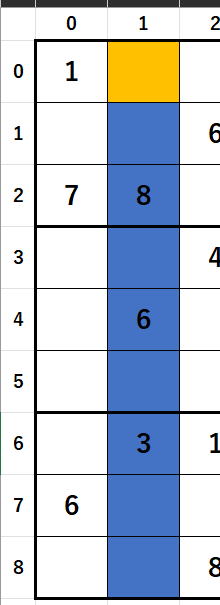を動かしていって8（すでに除外されていますが），6，3を除外します。{0,2,0,4,0,0,7,0,0}
最後にブロック
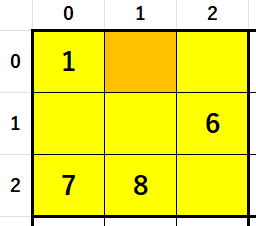を動かしていって、1，6（すでに除かれています），7，8（すでに除かれています）を外します。
{0,2,0,4,0,0,0,0,0}
座標（i，j）からブロックの先頭の座標（y，x）を作り出すには、
int y = 3 * (i / 3);
int x = 3 * (j / 3);
とします。
該当セル（4，7）からブロック先頭の座標（3，6）
を作り出すには
int y = 3 * (4 / 3);
int x = 3 * (6 / 3);
3 * (4 / 3) = 3 * 1 = 3
3 * (7 / 3) = 3 * 2 = 6
計算から、確かに（4，7）からブロック先頭の座標（3，6）が作り出せていることがわかると思います。
今回は、（0，1）から（0，0）を作るにはどうしたらよいですか。
なぜ、ブロック先頭の座標(y, x)の話をしているかと申しますと、
(y, x)から
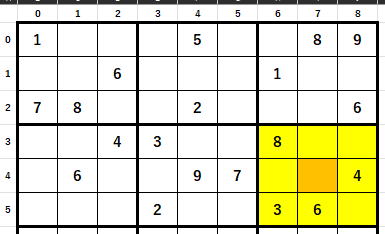黄色のセルの座標を作り出せるからです。次に、リストの個数を数えます。
mx[0][1] = 0;//候補数字いったん0に初期化しておく
0に初期化したことが威力を発揮して、
0も要りませんから{2,4}とすることができるのです。
それから私が苦戦を強いられたのは文字ずれです。
複数の場所で表示をさせていてどこを直せばよいのかわからずに苦戦しました。
そこで、
void hy();//コンソールに結果を表示させる関数
という関数を用意して表示はこの関数一本しました。
もっと見やすくするために横の間隔を調整しました。
第１話へ 第３話へ
トップへ