第12話 3次魔方陣自動生成

#include<iostream>
using namespace std;
void f(int s); //sは次元番号
int n; //次元数をキーボードから指定
int cn = 0; //順列を数える変数
int y[9] = { 0,1,2,0,2,0,1,1,2 };
int x[9] = { 0,1,2,2,0,1,0,2,1 };
int a[3][3];
int main() {
//cout << "n = ";
//scanf_s("%d", &n); //キーボードからnの値を取得
n = 9;
clock_t hj, ow;
hj = clock(); //始まりの時刻取得
f(0);
ow = clock(); //終わりの時刻取得
cout << "計算時間は" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl;
cout << "魔方陣は" << cn << "個できました。" << endl;
cout << "プロジェクト成功" << endl;
return(0);
}
void f(int s) {
for (int i = 1; i < n + 1; i++) {
if (s == 0) {
a[y[s]][x[s]] = i;
}
if (s > 0) {
for (int j = 0; j < s; j++) {
if (i == a[y[j]][x[j]])goto tobi;
}
a[y[s]][x[s]] = i;
if (s == 2) {
int w = 0;
for (int j = 0; j < 3; j++)w += a[j][j];//右下がり対角線合計算出
if (w != 15)goto tobi;
}
if (s == 4) {
int w = 0;
for (int j = 0; j < 3; j++)w += a[j][2 - j];//右上がり対角線合計算出
if (w != 15)goto tobi;
}
if (s == 5) {
int w = 0;
for (int j = 0; j < 3; j++)w += a[0][j];//1行目合計算出
if (w != 15)goto tobi;
}
if (s == 6) {
int w = 0;
for (int j = 0; j < 3; j++)w += a[j][0];//1列目合計算出
if (w != 15)goto tobi;
}
if (s == 7) {
int w = 0;
for (int j = 0; j < 3; j++)w += a[1][j];//2行目合計算出
if (w != 15)goto tobi;
w = 0;
for (int j = 0; j < 3; j++)w += a[j][2];//3列目合計算出
if (w != 15)goto tobi;
}
if (s == 8) {
int w = 0;
for (int j = 0; j < 3; j++)w += a[2][j];//3行目合計算出
if (w != 15)goto tobi;
w = 0;
for (int j = 0; j < 3; j++)w += a[j][1];//2列目合憲算出
if (w != 15)goto tobi;
}
}
if (s + 1 < n)f(s + 1); //1つ上(奥)の次元に飛翔
if (s + 1 == n) { //一番奥の部屋に到達!
for (int j = 0; j < 3; j++) {//魔方陣をコンソールに出力
for (int k = 0; k < 3; k++) {
cout << a[j][k] << " ";
}
cout << endl;
}
cout << endl;
cn++; //順列数をカウント
}
tobi:;
}
}
------------------------------------------------
本講では、
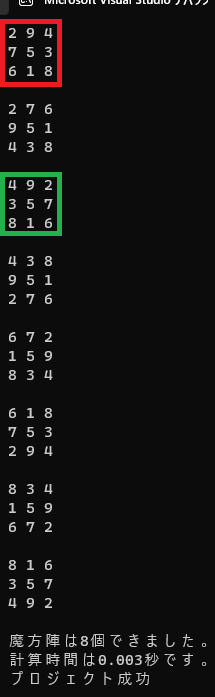
では8つを区別していますが、
数学者たちが数独を研究するときは、
上の8つを1つとカウントします。
緑は赤を左右対称移動したものです。
上下対称移動や点対称移動などによって、
重なるものを1個と考えるわけです。
ですが、人間は左右対称移動した数独は別のものと認識しますので、
本講では8つを別のものとしてカウントします。
------------------------------------------------
ヒント数0の数独を解くには、まだまだやるべきことがたくさんあります。
第3講試行錯誤法でヒント数0数独の解答を作る(2)へ第1話への課題を出します。
行・列・ブロックの重複は気にしないで、
2次元配列には、1~9までの数字を入れて、
ブロックがわかるように

図のように*を入れてください。
生成させるものは10個という条件をいれます。
これを改良していって、
①行重複をしない ②列重複をしない ③ブロック重複をしない
と条件を加えて行ってヒント数0の数独を生成させます。
第11話へ 第3講第1話へ
トップへ