第1話 *によってブロックがわかるようにする

コピペ用
#include<iostream>
#include<conio.h> //while (!_kbhit()); を使うためのお呪い。
using namespace std;
void f(int s); //sは次元番号=部屋番号
int n; //次元数(部屋数)をキーボードから指定
int cn = 0; //順列を数える変数
int a[9][9];//2次元配列
int main() {
//cout << "n = ";
//scanf_s("%d", &n); //キーボードからnの値を取得
n = 9; //将来16次数独・25次数独も視野に入れて
clock_t hj, ow;
hj = clock(); //始まりの時刻を取得
f(0); //本プロジェクトの核心部分
ow = clock(); //終わりの時刻を取得
cout << "計算時間は" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl;
cout << "順列の場合の数は" << cn << "です。" << endl;
cout << "プロジェクト成功" << endl;
while (!_kbhit()); //待機させるための命令
return(0);
}
void f(int s) {
a[s / 9][s % 9] = rand() % 9 + 1;
if (s + 1 < n)f(s + 1); //1つ上の次元に飛翔(1つ奥の部屋に入室)
if (s + 1 == n) { //一番奥の部屋に到達!
for (int j = 0; j < 12; j++)cout << "* "; //一本目の横線
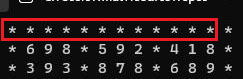
cout << "*"; //位置調整

cout << endl;
for (int j = 0; j < 9; j++) {
for (int k = 0; k < 9; k++) {
if (k % 3 == 0)cout << "* "; //

cout << a[j][k] << " "; //数独を表示
if (k == 8)cout << "* "; //位置調整

}
if (j % 3 == 2) {
cout << endl;
for (int j = 0; j < 12; j++)cout << "* "; //2本目・3本目・4本目の横線

cout << "*";
}
cout << endl;
}
cout << endl;
}
}
解説用
#include<iostream>
#include<conio.h> //while (!_kbhit()); を使うためのお呪い。
using namespace std;
void f(int s); //sは次元番号=部屋番号
int n; //次元数(部屋数)をキーボードから指定
int cn = 0; //順列を数える変数
int a[9][9];//2次元配列
int main() {
//cout << "n = ";
//scanf_s("%d", &n); //キーボードからnの値を取得
n = 9; //将来16次数独・25次数独も視野に入れて
clock_t hj, ow;
hj = clock(); //始まりの時刻を取得
f(0); //本プロジェクトの核心部分
ow = clock(); //終わりの時刻を取得
cout << "計算時間は" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl;
cout << "順列の場合の数は" << cn << "です。" << endl;
cout << "プロジェクト成功" << endl;
while (!_kbhit()); //待機させるための命令
return(0);
}
void f(int s) {
a[s / 9][s % 9] = rand() % 9 + 1;
if (s + 1 < n)f(s + 1); //1つ上の次元に飛翔(1つ奥の部屋に入室)
if (s + 1 == n) { //一番奥の部屋に到達!
for (int j = 0; j < 12; j++)cout << "* "; //一本目の横線
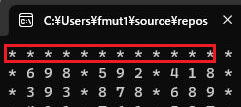
cout << "*"; //位置調整

cout << endl;
for (int j = 0; j < 9; j++) {
for (int k = 0; k < 9; k++) {
if (k % 3 == 0)cout << "* "; //位置調整 k = 0, k = 3, k = 6, k = 8
cout << a[j][k] << " "; //数独を表示
if (k == 8)cout << "* "; //位置調整
}
if (j % 3 == 2) {
cout << endl;
for (int j = 0; j < 12; j++)cout << "* "; //2本目・3本目・4本目の横線
cout << "*";
}
cout << endl;
}
cout << endl;
}
}
さて、いよいよ目的の数独解答自動生成アプリの開発に入りましょう。
これも段階を踏んでいきます。
ここでも新しい名称を導入します。
数字の重複を認めないという条件について
①行だけ満たすものを疑似疑似数独
(本当は疑似疑似疑似数独ですね。
解が複数ある時点で疑似がつきますから。
便宜上最初の疑似を省略します。)
②列も満たすものを疑似数独
とします。
③最後にブロックの条件を加えて、ヒント数0の数独を解くを実現させます。
まず、疑似疑似数独の開発をします。
いったん81次順列に戻して2次元に並べて、

・
・
・
 場合の数が100になったときにとめている。
場合の数が100になったときにとめている。これを改良して「①行だけ満たすものを疑似疑似数独」を実現します。
*の位置については粘り強く試行錯誤を繰り返して上の図になるようにしてください。
第2講第12話へ 第2話へ
トップへ