第11話 9次順列から3次魔方陣を生成させるにはどうしたらよいか?
#include<iostream>
using namespace std;
void f(int s); //sは次元番号=部屋番号
int n; //次元数(部屋数)をキーボードから指定
int cn = 0; //順列を数える変数
int a[10];//大きめにとった
int main() {
cout << "n = ";
scanf_s("%d", &n); //キーボードからnの値を取得
f(0);
cout << "順列の場合の数は" << cn << "です。" << endl;
cout << "プロジェクト成功" << endl;
return(0);
}
void f(int s) {
for (int i = 1; i < n + 1; i++) {
if (s == 0) {
a[s] = i;
}
if (s > 0) {
for (int j = 0; j < s; j++) {
if (i == a[j])goto tobi;
a[s] = i;
}
}
if (s + 1 < n)f(s + 1); //1つ上の次元に飛翔(1つ奥の部屋に入室)
if (s + 1 == n) { //一番奥の部屋に到達!
for (int j = 0; j < n; j++) { //順列を表示
cout << a[j] << " ";
}
cout << endl;
cn++; //順列数をカウント
}
tobi:;
}
}
n次順列自動生成を実行して、
n = 9
とすると

の状態が永遠と続きます。
これを2次元に並べて
3次魔方陣を生成させるなんて無理だと思いますよね。
何の工夫もしなければその通りです。
しかし、色々と工夫すると

0.003秒ですべての魔方陣を生成させることに成功しています。。
工夫とは入力順と行と列と対角線における合計を最後にやるのではなく、
必要なセルに到達したら合計算出をして15でなければ前の部屋に戻るようにさせればよいのです。
まず、入力順は

通常と異なり、(y、x)になっておりyは縦座標xは横座標
となっていることをご注意お願いします。
xとyの位置が取り違われているのは2次元配列が(行番号,列番号)となっているからです。
今回も部屋番号をsとします。
高校教諭時代ずっと時間割係をやっていましたが、
時間割を組には条件の厳しい駒から埋めていくという鉄則を設けてそれでやっていました。
体育(1時間目は体に悪い)・家庭科(お昼休みを含んでの調子実習)・習熟選択・非常勤(曜日や時間に制限)
などをあとに残したのでは、動かせないからです。
逆に、後に残りたものは単駒・選択ナシなどです。
これらは比較的動かせるからです。
場合の数でも制限・制約の厳しいところから始めるは、
やはり、鉄則です。対角線のセル(まる)は行合計・列合計対角線合計にかかわるので、

この条件をsの配置にするためには、
とするわけです。
6次魔方陣自動生成を研究していた頃に、
この入力順を採用したら何百倍から何万倍になった時には驚きまた。
int y[9] = { 0,1,2,0,2,0,1,1,2 };
int x[9] = { 0,1,2,2,0,1,0,2,1 };
という配列を考える必要があります。
そして、その部屋を現す2次元配列を
int a[3][3];
とします。
 によって、
によって、
入力順ができていることを
a[3][3]の添え字のところに具体的な数字をいれて動きを見てみましょう。
a[y[0]][x[0]] = a[0][0] a[y[1]][x[1]] = a[1][1] a[y[2]][x[2]] = a[2][2]
a[y[3]][x[3]] = a[0][2] a[y[4]][x[4]] = a[2][0] a[y[5]][x[5]] = a[0][1]
a[y[6]][x[6]] = a[1][0] a[y[7]][x[7]] = a[1][2] a[y[8]][x[8]] = a[2][1]
どうですか。見事に

部屋番号を実現しています。
最後に、合計チェックをするマスを確認します。
合計を計算するのは、3つのマスに数字が入っているときのみという点にご注意お願いします。

2のときには右下がり対角線(0,0)、(1,1)、(2,2)上に3マスにお客さんが3人に並んでおり、
右下がり対角線の合計を算出する必要があります。
部屋2(2,2)においてチェックしないと
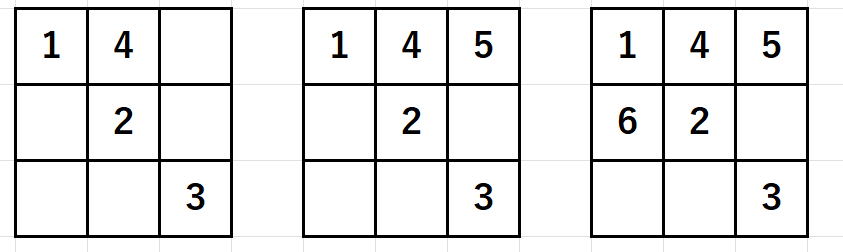
などと進んでしまいます。
2(2,2)の位置で右下がり合計を計算して15になっていないときには元の次元にもどるように設定しておけば、
1つ手前1(0,0)に戻り

と動かしていけば右下がり対角線合計が15になる場合を比較的簡単に見出すことに成功するわけです。
(2,2)に関門を置いておけば無駄な探索が行われないですむということが、
お分かりかと思います。
---------------------------------------------------------------
尚、対角線合計・行合計・列合計が15になるのは次の計算から明らかです。
(1+2+3+4+5+6+7+8+9)÷3 = 15
3で割るのは3行や3列からです。
すべての数の和を3で割れば、各行・各列・各対角線の合計が算出できるわけです。
---------------------------------------------------------------

同様にして関門は4(2,2)、5(0,1)、6(1,0)、7(1,2)、8(2,1)に
置く必要があることがわかると思います。
色のついている関門は
4(2,2)右下がり対角線合計・5(0,1)1行目合計・6(1,0)2列目合計および2行目合計・
7(1,2)2行目合計および3列目合計・8(2,1)3行目合計および2列目合計
をすることを任務とします。
でが、皆さんn次順列自動生成プログラムを改良して
 魔方陣自動生成プログラムを実現しましょう。
魔方陣自動生成プログラムを実現しましょう。第10話へ 第12話へ
トップへ