Æ┤ŖgæÕāsā^āSāēāXÉö¢ŌæĶ
éüüCééüCéāéŚLŚØÉöéŲéĘéķéŲé½üA
![]()
é═üAÉ«ÉöēüiÄ®æRÉöēéÓŖ▄é▐üjééÓé┬é┼éĀéļéżé®üBŚ]īĘÆĶŚØé╔é©é»éķÄ®æRÉöē¢ŌæĶüiŖgæÕ╦▀└║▐ūĮÉö¢ŌæĶüjéÄĶé¬é®éĶé╔üAé▒é╠¢ŌæĶéŹlé”é─é▌éµéżüBŖgæÕ╦▀└║▐ūĮÉöé┼é═üAłĻé┬é¬ö}ēŅĢŽÉöā┐é╠łĻĤŖųÉöé┼üAæ╝é╠ō±é┬é═ā┐é╠ō±Ä¤ŖųÉöéŲé╚é┴éĮüB
ü@é╗é▒é┼üA![]() éŲé©éóé─é▌éµéżüBéĘéķéŲüA
éŲé©éóé─é▌éµéżüBéĘéķéŲüA
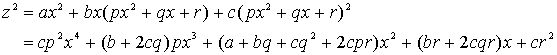
é▒éĻé¬üAŖ«æSĢĮĢ¹é╔é╚éķéµéżé╔üA
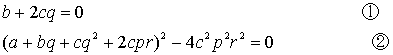
éŲé©éŁüBéµé┴é─![]() üA
üA
![]()
é▒é▒é┼![]() éŲé©é»é╬üA
éŲé©é»é╬üA
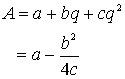
é▄éĮüAćAé®éń
![]()
éĘé╚éĒé┐üA
![]()
![]()
éµé┴é─üA![]() é╚éńé╬
é╚éńé╬
![]() éĘé╚éĒé┐üA
éĘé╚éĒé┐üA
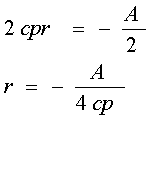
éĄéĮé¬é┴é─üA![]()
éõé”é╔üA
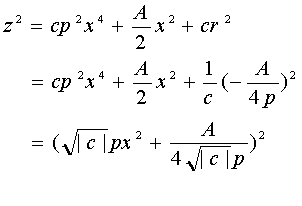
éµé┴é─üAéÜüäéOüCéśüäéOüCéÖüäéOüiÉ│é╠ŚLŚØÉöüjé╔ī└ÆĶéĘéķéŲüA
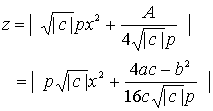
Å\Ģ¬æÕé½éóéśé▄éĮé═Å\Ģ¬Å¼é│éóéśé╔æ╬éĄé─
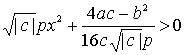
é¢×éĮéĘé®éńüA
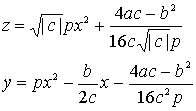
éÉüäéOéŲéĄé─Ś╝Ģėé╔![]() éé®é»é─üA
éé®é»é─üA
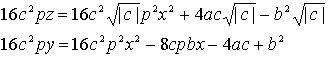
éµé┴é─üA![]() é┼éāé¬ĢĮĢ¹Éöé╚éńé╬
é┼éāé¬ĢĮĢ¹Éöé╚éńé╬
![]() é═
é═
![]()
é╠É│é╠ŚLŚØÉöēé┼éĀéĶüAéÉéŌéśé╔ē×éČé─¢│ī└é╔æČŹ▌éĘéķüBé╗éĄé─üA![]() é╠Ģ¬ĢĻé╠ī÷ö{Éöéé®é»éĻé╬üAÄ®æRÉöēéŲé╚éķé╠é┼üAÄ®æRÉöēé═¢│ī└é╔æČŹ▌éĘéķüB
é╠Ģ¬ĢĻé╠ī÷ö{Éöéé®é»éĻé╬üAÄ®æRÉöēéŲé╚éķé╠é┼üAÄ®æRÉöēé═¢│ī└é╔æČŹ▌éĘéķüB
é╗éĻé┼é═éóéŁé┬é®é╠Ä®æRÉöēéÄ”éĘé▒éŲé╔éĄéµéżüB
ćTü@éüüüéQüCééüüéRüCéāüüéPé╠éŲé½
ü@![]()
éÉüüéPéŲéĘéķéŲ
ü@![]()
ć@
éśüüéQé╠éŲé½üAüiéRéQüCéPéVüCéUéRüj
ćA
éśüüéRé╠éŲé½üAüiéSéWüCéVéRüCéPéSéRüj
ćB
éśüüéSé╠éŲé½üAüiéUéSüCéPéUéPüCéQéTéTüj
ćC
éśüüéTé╠éŲé½üAüiéWéOüCéQéWéPüCéRéXéXüj
ćD
éśüüéUé╠éŲé½üAüiéXéUüCéSéRéRüCéTéVéTüj
éÉüüéQéŲéĘéķéŲüA
![]()
ć@
éśüüéRé╠éŲé½üAüiéXéUüCéSéRéRüCéTéVéTüj
ćA
éśüüéSé╠éŲé½üAüiéPéQéWüCéWéRéRüCéPéOéQéRüj
ćB
éśüüéTé╠éŲé½üAüiéPéUéOüCéPéRéUéPüCéPéTéXéXüj
ćC
éśüüéUé╠éŲé½üAüiéPéXéQüCéQéOéPéVüCéQéRéOéRüj
ćD
éśüüéVé╠éŲé½üAüiéQéQéSüCéQéWéOéPüCéRéPéRéTüj
ćUü@éüüüü|éQüCééüüéTüCéāüüéPé╠éŲé½
![]()
éÉüüéPé╠éŲé½
![]()
ć@
éśüüéQé╠éŲé½üAüiéRéQüCéPéVüCéRéPüj
ćA
éśüüéRé╠éŲé½üAüiéSéWüCéTéVüCéPéPéPüj
ćB
éśüüéSé╠éŲé½üAüiéUéSüCéPéQéXüCéQéQéRüj
ćC
éśüüéTé╠éŲé½üAüiéWéOüCéQéRéRüCéRéUéVüj
ćD
éśüüéUé╠éŲé½üAüiéXéUüCéRéUéXüCéTéSéRüj
éÉüüéQé╠éŲé½üA
![]()
ć@
éśüüéPé╠éŲé½üAüiéRéQüCéPéVüCéRéPüj
ćA
éśüüéQé╠éŲé½üAüiéUéSüCéPéQéXüCéQéQéRüj
ćB
éśüüéRé╠éŲé½üAüiéXéUüCéRéUéXüCéTéSéRüj
ćC
éśüüéSé╠éŲé½üAüiéPéQéWüCéVéRéVüCéXéXéPüj
ćD
éśüüéTé╠éŲé½üAüiéPéUéOüCéPéQéRéRüCéPéTéUéVüj
ćVü@éüüüéRüCééüüü|éPüCéāüüéSé╠éŲé½üA
![]()
éÉüüéPéŲéĘéķéŲüA
![]()
ć@
éśüüéPé╠éŲé½üAüiéQéTéUüCéQéSéPüCéUéOéUüj
ćA
éśüüéQé╠éŲé½üAüiéTéPéQüCéPéOéSéPüCéQéPéSéQüj
ćB
éśüüéRé╠éŲé½üAüiéVéUéWüCéQéRéTéRüCéSéVéOéQüj
