今までの講義に比べると、
かなり難しいかも知れません。
さて、今回のプログラムを考える前に、
前話で解説していない重要な話があります。
それは、
i=jまたはi=5−jという条件の否定は、
i<>jかつi<>5−jであるということです。
一般に、条件
pまたはq
の否定は、
(pでない)かつ(qでない)
になります。
また、pかつqの否定は
(pでない)または(qでない)
となります。
「かつ」という言葉に聞き慣れていない人もいると思いますが、
pかつq
は条件pも条件qも同時に満たすことを表します。
それに対して、
pまたはq
は条件pを満たすか、条件qを満たしていればよいのです。
どちらか一方の条件を満たしていればよいのですから、
両方の条件を満たすpかつqの状態でもいいのです。
集合の図を書いてみましょう。
条件pを満たす集合をP、
条件qを満たす集合をQ、
pかつqを満たす集合をP∩Q、
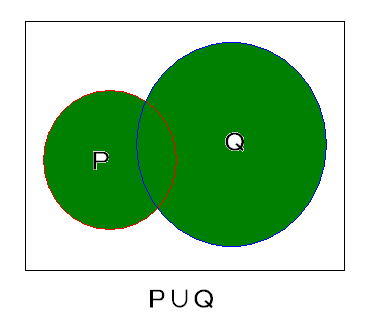
pまたはqを満たす集合をP∪Qと表すことにしますと、
下図のようになります。
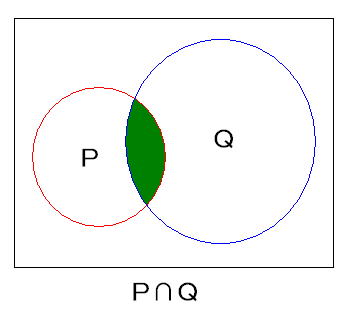
したがって、条件pまたはqの否定を表す集合は、
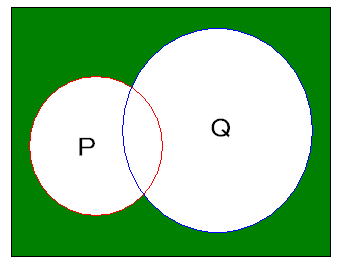
となり、条件pまたはqの否定は(pでない)かつ(qでない)となります。
また、条件pかつqの否定を表す集合は、