第5講 問題における数字の配置をいかにするか? 第2話 互いに素と均等な配置がどうして結びつくの?
均等に配置するということと互いに素は一見無関係なように見えます。
11 18 25 32 39 46 53 60 67
74 0 7 14 21 28 35 42 49
56 63 70 77 3 10 17 24 31
38 45 52 59 66 73 80 6 13
20 27 34 41 48 55 62 69 76
2 9 16 23 30 37 44 51 58
65 72 79 5 12 19 26 33 40
47 54 61 68 75 1 8 15 22
29 36 43 50 57 64 71 78 4
始めは任意で何でもよく、
11 18 25 32 39 46 53 60 67
74 0 7 14 21 28 35 42 49
56 63 70 77 3 10 17 24 31
38 45 52 59 66 73 80 6 13
20 27 34 41 48 55 62 69 76
2 9 16 23 30 37 44 51 58
65 72 79 5 12 19 26 33 40
47 54 61 68 75 1 8 15 22
29 36 43 50 57 64 71 78 4
ピンクのセル番号にだけ数字を配置すればよいのです。添付ファイル
第1話へ 第3話へ トップへ

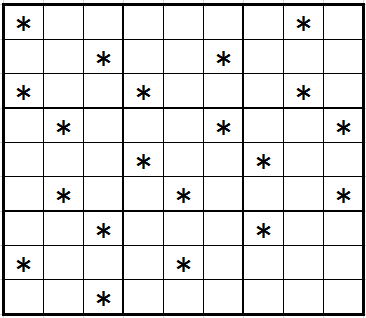
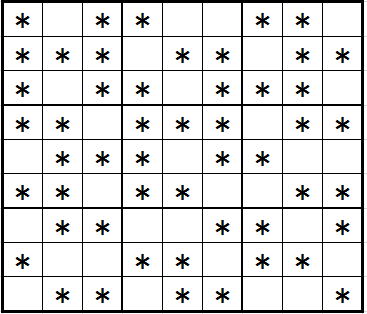
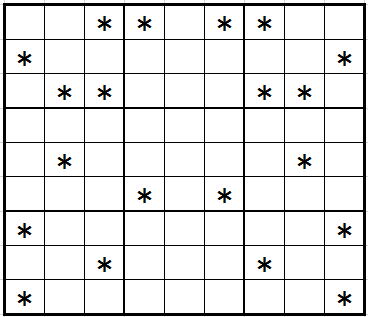
 を実現してください。
を実現してください。