第5講 問題における数字の配置をいかにするか?
第1話 互いに素について
ここ10年ぐらいでナンプレ自動生成ソフトの性能が上がったのは、
数理統計学を研究に活かしたからだそうです。
ヒントになる数字を配置するわけですが、
この配置によって出来る確率が決定されています。
よい配置なら短時間で出来る可能性が高くなり、
悪ければ時間をかけても出来ない可能性が生じます。
理想的な配置は全体にヒントが均等に配置される場合です。
例えば、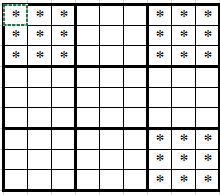 のように偏った配置では下手をすると生成に30分程度要してしまいます。
のように偏った配置では下手をすると生成に30分程度要してしまいます。
では、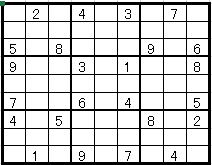 のように均等に数字を配置するにはどうしたらよいでしょうか。
のように均等に数字を配置するにはどうしたらよいでしょうか。
私は、この配置は整数論を使ってやっています。
整数論といっても中学から高校にかけての整数の単元にすぎず決して難しいものではありません。
皆さん、互いに素ということを学んだことを覚えていますか。
互いに素とは(a,b)を分数a/bにしたときに約分できない場合を指します。
言いかえると(a,b)の最大公約数が1であるときに、aとbは互いに素であるというのです。
ですから、互いに素であるものと互いに素でないものをそれぞれ例示すると、
(5,2)と(6,2)です。
(6,2)の方は最大公約数が2であるのに対して、
(5,2)の方は最大公約数が1ですね。
互いに素である場合に大変面白い性質があり、
それを利用して魔方陣の自動生成に活かしたことがあります。
魔方陣を作成する方法の1つに、
ラテン方陣を2つ作って組み合わせるというものがあります。
ラテン方陣とは数独の素になったもので、
5次ラテン方陣なら1,2,3,4,5という数字が、
すべての行にもすべての列にもひとつずつ並ぶものです。
魔方陣を作成するときには、さらに対角線上にもひとつずつ並ぶものを利用します。
ラテン方陣にしてかつ対角線上にも数字の重複がないものを作り出すことは、
5次や7次なら簡単ですが、4次や6次では難しくなります。
対角線の条件を満たす5次ラテン方陣は次のような簡単な方法で出来ます。
12345という数字を用意しておいて2つずらしを行うだけでできます。
| 1 |
2 |
3 |
4 |
5 |
| 4 |
5 |
1 |
2 |
3 |
| 2 |
3 |
4 |
5 |
1 |
| 5 |
1 |
2 |
3 |
4 |
| 3 |
4 |
5 |
1 |
2 |
どの行にもどの列にもいずれの対角線上にも、
1から5までの数字がひとつずつ並んでいますね。
2つずらすという意味は1の位置を見ればわかりますね。
2つずつ右にずれていっています。
3つずらしをいっても対角線の条件を満たすラテン方陣になります。
| 1 |
2 |
3 |
4 |
5 |
| 3 |
4 |
5 |
1 |
2 |
| 5 |
1 |
2 |
3 |
4 |
| 2 |
3 |
4 |
5 |
1 |
| 4 |
5 |
1 |
2 |
3 |
5次魔方陣を作るには、2つの対角線の重複を許さないラテン方陣を次のように合体すればよいのです。
1番目のラテン方陣の各数字に2番目のラテン方陣の同位置の数字から1引いてから5をかけたものを足します。
ピンクのセルを例にすると、
5+(4-1)×5=20
です。すべてのセルについて同じことをやりますと、
| 1 |
7 |
13 |
19 |
25 |
| 14 |
20 |
21 |
2 |
8 |
| 22 |
3 |
9 |
15 |
16 |
| 10 |
11 |
17 |
23 |
4 |
| 18 |
24 |
5 |
6 |
12 |
という方陣が出来ますが、
これは魔方陣ですね。
どの行合計も列合計も対角線合計も同じ65になっていますね。
7次魔方陣や11次魔方陣も同様な方法で簡単にできてしまいます。
ところが、4次や6次などの偶数では同じ方法では出来ないのです。
実際に、123456という数字を用意して同じことをやってみましょう。
| 1 |
2 |
3 |
4 |
5 |
6 |
| 5 |
6 |
1 |
2 |
3 |
4 |
| 3 |
4 |
5 |
6 |
1 |
2 |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 5 |
6 |
1 |
2 |
3 |
4 |
| 3 |
4 |
5 |
6 |
1 |
2 |
行はもちろんひとつずつ並ぶという条件を満たしていますが、
列は153153,264264,315315,426426,531531,642642
となりいずれも1から6までの数字がひとつずつ並ぶという条件を満たしていません。
3ずらしをしても、
| 1 |
2 |
3 |
4 |
5 |
6 |
| 4 |
5 |
6 |
1 |
2 |
3 |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 4 |
5 |
6 |
1 |
2 |
3 |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 4 |
5 |
6 |
1 |
2 |
3 |
もっとだめになります。どの列にも同じ数字が3回重複してしまいます。
5なら2つずらしや3つずらしをすれば対角線上の数字も重複しないラテン方陣になるのに、
6では列にも対角線にも重複が発生していまいます。
なぜ5と6でこんなに大きな違いがあるのでしょうか。
ヒントは(5,2)と(6,2)です。
2はずらしに対応しています。
5と2は互いに素であるのに対して、
6と2は互いに素ではありません。
対角線の条件を考えなければ5の場合には、
1ずらしでも2ずらしでも3ずらしでも4ずらしでもラテン方陣になるのに対して、
6の場合は1ずらしと5ずらし以外はラテン方陣になりません。
(6,1)と(6,5)は互いに素であるのに対して、
(6,2),(6,3),(6,4)は互いに素ではないからです。
魔方陣場合には対角線上も数字が重複してはならないので、
1ずらしやn-1ずらしは最初からだめなのです。
ですから、(6,2),(6,3),(6,4)のようなずらし方でラテン方陣にならなければ、
魔方陣は出来ないのです。
さて、 のように均等に配置することと、
のように均等に配置することと、
互いに素はいかにして結びつくのでしょうか。
第4講第10話へ 第2話へ
トップへ
 のように偏った配置では下手をすると生成に30分程度要してしまいます。
のように偏った配置では下手をすると生成に30分程度要してしまいます。 のように均等に数字を配置するにはどうしたらよいでしょうか。
のように均等に数字を配置するにはどうしたらよいでしょうか。