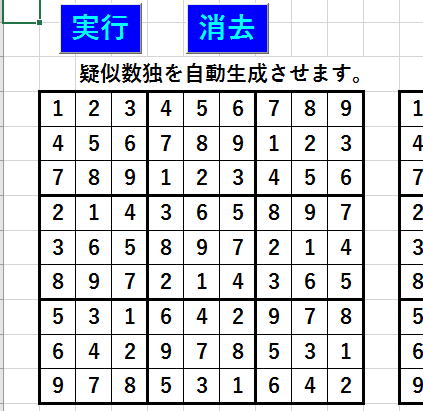
第３講 試行錯誤法でヒント数０数独の解答を作る（２）
第５話 数独解答自動生成アプリ
を実現するプログラム例
Dim n As Byte, m(8, 8) As Byte, cn As Integer 'nは数独の一辺、x(15)は数独を収納する配列、cnは数独総数をカウントする変数
Private Sub CommandButton1_Click()
CommandButton2_Click
n = 9 '縦横を9にしている
cn = 0
f (0) '数独作成プロシージャ
End Sub
Sub f(g As Byte)
Dim i As Byte, j As Byte, h As Byte, a As Integer, s As Integer, w As Byte
Dim y As Byte, x As Byte
y = Int(g / n)
x = g Mod n
a = cn Mod 10
s = Int(cn / 10)
For i = 0 To n - 1
m(y, x) = i + 1 '1から9までの数字を代入
h = 1
If x > 0 Then '行の重複を検査して、重複がある場合にはhを0として以下の処理をさせない。
For j = 0 To x - 1
If m(y, x) = m(y, j) Then
h = 0
Exit For
End If
Next
End If
If y > 0 Then '行の重複を検査して、重複がある場合にはhを0として以下の処理をさせない。
For j = 0 To y - 1
If m(y, x) = m(j, x) Then
h = 0
Exit For
End If
Next
End If
If h = 1 And y > 0 Then 'ブロックの重複を検査して、重複がある場合にはhを0として以下の処理をさせない。
For j = 0 To n - 1
xx = 3 * Int(x / 3) + (j Mod 3)
yy = 3 * Int(y / 3) + Int(j / 3)
If x = xx And y = yy Then Exit For
If x <> xx And y <> yy Then
If m(yy, xx) = m(y, x) Then
h = 0
Exit For
End If
End If
Next
End If
If h = 1 Then
If g + 1 < n * n Then '行・列・ブロックの重複がなく、g + 1がn * n以下のときに、次のセル番号の世界に飛ぶ
f (g + 1)
If cn = 10 Then Exit Sub '数独が10個生成した段階で探索をやめさせている。
Else
For j = 0 To n * n - 1 '数独が出来たのでシートに表示させている。
Cells(4 + Int(j / n) + (n + 1) * s, 2 + (j Mod n) + (n + 1) * a) = m(Int(j / n), (j Mod n))
Next
cn = cn + 1 '数独総数カウント
If cn = 10 Then Exit Sub '数独が10個生成した段階で探索をやめさせている。
End If
End If
Next
End Sub
Private Sub CommandButton2_Click()
Rows("4:30000").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
今回は、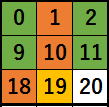
オレンジを重複検査の対象から外しましたが、
対象にするのがよいのか、
対象にしない方がよいのか実験で決めましょう。
１０個程度の生成では差は出ませんので、
If cn = 10 Then Exit Sub
の10を10000に変更して両方の生成にかかる時間を調べて下さい。
時間を調べるには
Private Sub CommandButton1_Click()
CommandButton2_Click
n = 9
cn = 0
hj = Timer
f (0) 'ｎ次順列作成プロシージャ
Cells(3, 2) = "１万個生成するのにかかった時間は"
Cells(3, 12) = Timer - hj
Cells(3, 13) = "秒です。"
End Sub
とすればよいですね。
For j = 0 To n * n - 1
Cells(4 + Int(j / n) + (n + 1) * s, 2 + (j Mod n) + (n + 1) * a) = m(Int(j / n), (j Mod n))
Next
は削除するか、REM文にしておいてください。
これがあると作成速度が著しく落ちるからです。
まだたいして工夫もしていない段階で
１個あたり
６．６÷１００００＝０．０００６６秒です。
いかに速いかわかります。
でも、後に改良してもっと速くします。
