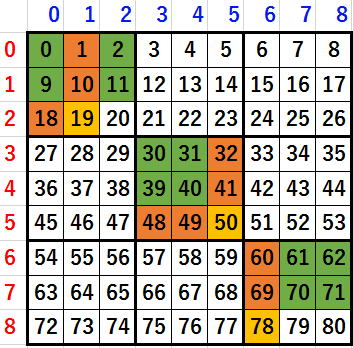
ブロックの重複検査をしなければならないセルは、
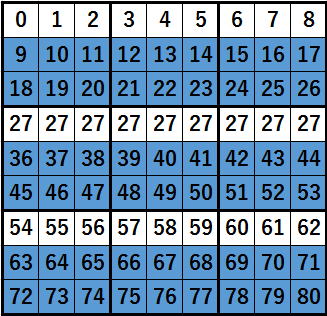
色を塗ったところです。
セル番号9すでに列検査で済んでいるはずだから、
要らないはずだとお考えの方はかなり慧眼な人です。
ところが、必要なのです。
9は1と2との重複検査をしなければなりませんね。
10については1との重複検査は列のときの重複検査に済んでいますし、
9との重複検査は行のときの重複検査で済んでいますから、
必要なのは、0と2です。
20なら必要なのは、0，1，9，10です。
場所によって違い一見共通の法則がないように見えますが、
逆に検査のいらない場所に色を塗ると、
共通性が見えてきます。
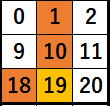
19についてみたときに、
オレンジが検査済みの場所です。
つまり、検査が必要なセルは、
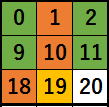
緑です。
共通する法則は、検査するセルは過去（セル番号が若い）のセルであり、
かつ同じ行上にも列上にもないセルということになります。
尚、オレンジを含めて検査してもたいした違いがないと、
主張する方もいらっしゃると思います。
ですが、速度＝スピードが命である数独自動作成アプリでは、
やはり無駄はしない方がよいと思います。
ただ、たいした違いがないという主張にも一理あります。
なぜなら、オレンジを重複検査対象から外すためには、
If文を使わなければならないからです。
対象から外すのにかかる時間と無駄な検査の時間のどちらが短いのかによって決まるのです。
ですから、オレンジを対象から外した方がよいか、
対象にした方がよいかは、実験してみなければわからないのです。
後に実験することにして、とりあえずはオレンジを検査対象から外すことにして進めましょう。
では、
19と0,2,9,11が同じブロックにあることや、
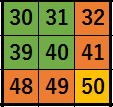50と30,31,39,40が同じブロックにあることなどは、どのように認識させたらよいのでしょうか。
同じブロックにあることは
※普通座標は（横座標，縦座標）ですが、２次元配列配列が（縦，横）となっていますので、
これに合わせて座標を（縦座標，横座標）としていることに注意して下さい。
すなわち、（ｘ，ｙ）ではなく（ｙ，ｘ）です。
座標(2,1)から(0,0)を
座標(5,5)から(3,3)を
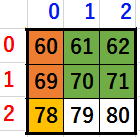
座標(8,6)から(6,6)を
（色が少し異なりますが、
と0を対応させているつもりです）作り出せれるかが鍵となります。
それが出来れば、
座標(0,0)から(0,0)を
座標(0,2)から(0,0)を
座標(1,0)から(0,0)を
座標(1,1)から(0,0)を
座標(3,3)から(3,3)を
座標(3,4)から(3,3)を
座標(4,3)から(3,3)を
座標(4,4)から(3,3)を
座標(6,7)から(6,6)を
座標(6,8)から(6,6)を
座標(7,7)から(6,6)を
座標(7,8)から(6,6)を
同じ方法で作り出すことが出来るはずです。
同じブロックにあるかは、
座標（ｙ、ｘ）からブロックの先頭座標（ｙ0，ｘ0）を作り出せるかで判定できることになります。
作り出せれば、同じブロックにあることになり、作り出せなければ異なるブロックということになります。
では、例えば、7から6を作り出すにはどうしたらよいですか。
答えは、
3 * Int(7 / 3) = 6
です。
8から6を作り出すのも同じ原理です。
3 * Int(8 / 3) = 6
つまり、y座標もx座標も作り方は同じということです。
最後にブロックの中を動かすには
For j=0 to 2
For k=0 to 2
・・・
If ・ Then goto tobi
Next
Next
tobi:
としてもよいのですが、
１次元For文で実現できることもヒントとして加えておきましょう。
For j=0 to 8
・・・
If ・ Then Exit For
Next
Exit Forがあるのは、比較を過去に限定するためです。
ブロック内の
ｙ座標にするにはInt(j / 3)
ｘ座標にするにj mod 3を使います。
ブロックの先頭座標を作り出すことによる効果は、
比較しようとしているセルが同ブロックにあるかないかを判定できるだけでなく、
先頭座標を使ってブロック内を動かすことが出来ることにもあります。
では、皆さん数独解答自動生成に挑戦しましょう。
