第７話 問題から解答を作るを実現するための課題
第８講の途中ですが、
ここから本講義に第２部に入ります。
第１部は解答から問題を作るでしたが、
第２部では先に問題を作り、
それを解いて唯一解なら問題と解答をCVSファイルに排出するわけです。
関数ｆで問題を作り、関数sudokukaihoで解いていきます。
ですから、役割が前と異なるために、
sudoku[A][y][x]を問題にして、
gensudoku[A][y][x]を解答に割り当てます。
したがいまして、mondai[A][y][x]はsudoku[A][y][x]から始まり、
順調にいけば解答となります。
mondai[A][y][x]はsudokukaihoの一番奥の部屋から戻っていく際に、
また姿を変えて最終的にはsudoku[A][y][x]に一致します。
ですから、mondai[A][y][x]が解答でいられるのはほんの一瞬のみであり、
一番奥の部屋に到達したときに、
mondai[A][y][x]からgensudoku[A][y][x]へのコピーしないと、
せっかくできた解答が消えてしまいます。
関数の再帰的使用をしていますから、
戻っていく過程でお掃除をして全体リスト解析もsudoku[A][y][x]の状態に
戻さなければならないからです。
では、順調にいかないとはどういうことでしょうか。
前回は、解答から問題を作りましたから解が存在するということは最初から分かっています。
ですが、今回は先に問題を作っていますから、
解が存在しないまたは複数解の可能性があります。
唯一解であるためには、cn1[a]が１でなければなりません。
ですから、
void hontai(void* aa) {
int a = *(int*)aa;
srand(u - 19 * a);
while (1) {
if (keizoku == 0)return;
zahyousakusei(a);
syokika(a);
f(a, 0);
for (char i = 0; i < n; i++) {
for (char j = 0; j < n; j++) {
mondai[a][i][j] = sudoku[a][i][j];
}
}
sudokukaiho(a, hnt);//数独を解くエンジン 部分構造解析を進めながら問題を解いていく
if (keizoku == 0)return;
if (cn1[a] == 1) {
if (H == 1) {
A = a;
H = 0;
}
keizoku = 0;
return;
}
}
}
としておいて、
解が存在しない場合にも複数解の場合にもスレッドは探索を続けなければなりません。
問題から解答を作るの機会に、
問題があるとわかっていながら放置していた問題点を解消することにしましょう。
void sudokukaiho(char a, char g) {//数独を解くエンジン
nextcell(a, g);//座標(Y[a][g], X[a][g])の取得
if (keizoku[a] == 0) {
for (char v = 0; v < th; v++)keizoku[v] = 0;
return;
}//数独を発見したスレッドからの連絡および閉じよの指令
for (char i = 0; i < mx[a][Y[a][g]][X[a][g]]; i++) {
if (keizoku[a] == 0) {
for (char v = 0; v < th; v++)keizoku[v] = 0;
return;
}//数独を発見したスレッドからの連絡および閉じよの指令
mondai[a][Y[a][g]][X[a][g]] = lst[a][Y[a][g]][X[a][g]][i];
//候補の数字を代入 例えば、mondai[0][1]なら{2, 4}の2，4の順に代入する
for (char j = 0; j < n; j++)if (j != X[a][g])if (mondai[a][Y[a][g]][j] == 0)kyokusyokaiseki(a, Y[a][g], j);
//x[Y[a][g]][X[a][g]]と同じ行にあるセルの単セル解析（候補数字探索）
if (keizoku[a] == 0) {
for (char v = 0; v < th; v++)keizoku[v] = 0;
return;
}//数独を発見したスレッドからの連絡および閉じよの指令
for (char j = 0; j < n; j++)if (j != Y[a][g])if (mondai[a][j][X[a][g]] == 0)kyokusyokaiseki(a, j, X[a][g]);
//x[Y[a][g]][X[a][g]]と同じ列にあるセルの単セル解析（候補数字探索）
if (keizoku[a] == 0) {
for (char v = 0; v < th; v++)keizoku[v] = 0;
return;
}//数独を発見したスレッドからの連絡および閉じよの指令
char s = 3 * (Y[a][g] / 3);
char t = 3 * (X[a][g] / 3);
for (char j = 0; j < n; j++) {
if (keizoku[a] == 0) {
for (char v = 0; v < th; v++)keizoku[v] = 0;
return;
}//数独を発見したスレッドからの連絡および閉じよの指令
if (s + (j / 3) != Y[a][g] && t + (j % 3) != X[a][g]) {//行解析と列解析と重複させないため
if (mondai[a][s + (j / 3)][t + (j % 3)] == 0) {
kyokusyokaiseki(a, s + (j / 3), t + (j % 3));
//x[Y[a][g]][X[a][g]]と同じブロックにあるセルの単セル解析（候補数字探索）
}
}
}
if (g + 1 < tm)sudokukaiho(a, g + 1);//内側部屋へ
if (cn1[a] == 2) {
return;//複数解
}
if (keizoku[a] == 0) {
for (char v = 0; v < th; v++)keizoku[v] = 0;
return;
}//数独を発見したスレッドからの連絡および閉じよの指令
if (g == tm - 1) {
for (char i = 0; i < n; i++) {
for (char j = 0; j < n; j++) {
if (mondai[a][i][j] != sudoku[a][i][j]) {
cn1[a] = 2;
return;
}
}
}
cn1[a]++;
}
if (i == mx[a][Y[a][g]][X[a][g]] - 1) {
//i < mx[a][Y[a][g]][X[a][g]] - 1)のときはiが１つ進んで上で単セル解析（候補数字探索）を行うので
//キャンセルは不要だが、最後だけはキャンセルをしなければならないので単セル解析（候補数字探 //索）を行う必要がある
//cout << "*-*-*-*-復元-*-*-*-*-*" << endl;
mondai[a][Y[a][g]][X[a][g]] = 0;
//cout << g << endl;
for (char j = 0; j < n; j++)if (j != X[a][g])if (mondai[a][Y[a][g]][j] == 0)kyokusyokaiseki(a, Y[a][g], j);
for (char j = 0; j < n; j++)if (j != Y[a][g])if (mondai[a][j][X[a][g]] == 0)kyokusyokaiseki(a, j, X[a][g]);
for (char j = 0; j < n; j++) {
if (s + (j / 3) != Y[a][g] && t + (j % 3) != X[a][g]) {
if (mondai[a][s + (j / 3)][t + (j % 3)] == 0) {
kyokusyokaiseki(a, s + (j / 3), t + (j % 3));
}
}
}
}
}
}
青になっている場所が問題個所です。
過剰解析になっていることがお判りでしょうか。
例えば
赤色の2を入力した際の部分解析は、
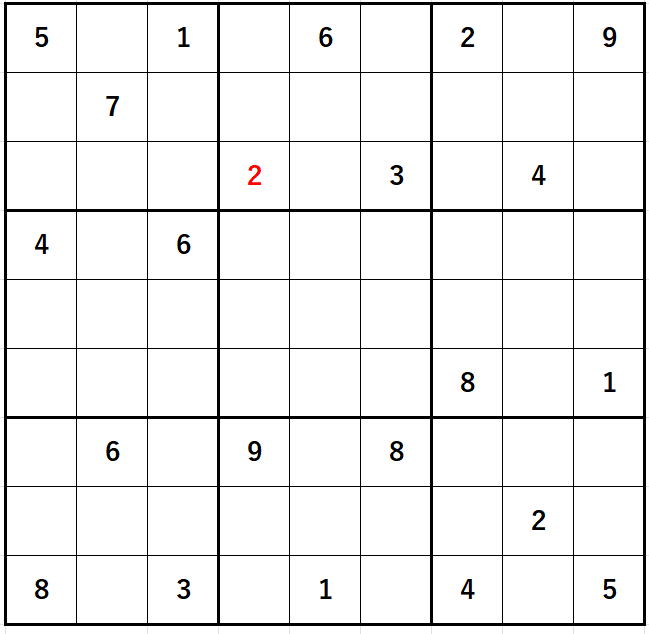
青の部分に限定されるべきですが、
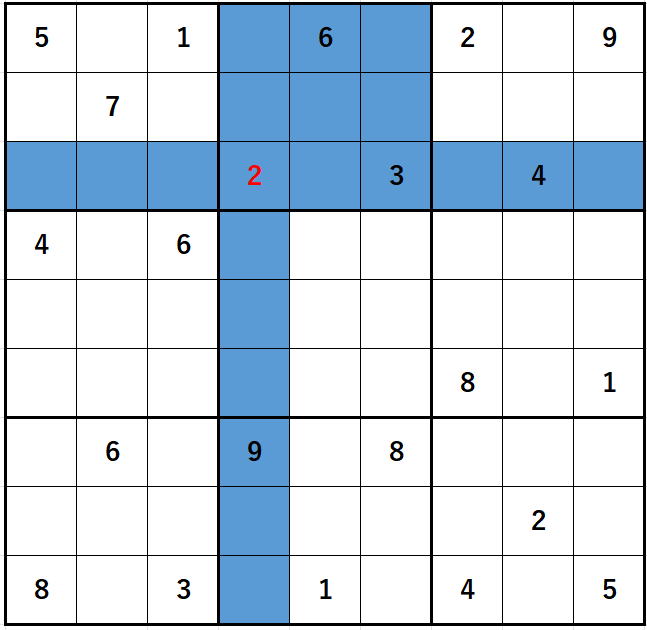（現実には青の中の空欄です）現行版
void kyokusyokaiseki(char a, char y, char x) {//局所解析 = 単セルリスト構造解析
for (char i = 0; i < n; i++)lst[a][y][x][i] = i + 1;//初期化{1,2,3,4,5,6,7,8,9}とする
mx[a][y][x] = 0;//{1,2,3,4,5,6,7,8,9}を{2,4}等にするために0に初期化 再カウントのため
for (char i = 0; i < n; i++) {//sudoku[a][y][x]と同じ行にあるセルからの影響を調べる
if (i != x) {//自分自身は対象にしない
if (sudoku[a][y][i] > 0) {//数字が入っている欄のみを対象とする
for (char j = 0; j < n; j++) {
if (lst[a][y][x][j] == sudoku[a][y][i])lst[a][y][x][j] = 0;
//sudoku[a][y][i]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (char i = 0; i < n; i++) {//sudoku[a][y][x]と同じ列にあるセルからの影響を調べる
if (i != y) {
if (sudoku[a][i][x] > 0) {//数字が入っている欄のみを対象とする
for (char j = 0; j < n; j++) {
if (lst[a][y][x][j] == sudoku[a][i][x])lst[a][y][x][j] = 0;
//sudoku[a][i][x]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (char i = 0; i < n; i++) {//sudoku[a][y][x]と同じブロックにあるセルからの影響を調べる
char yy = 3 * (y / 3) + (i / 3);
char xx = 3 * (x / 3) + (i % 3);
if (yy != y && xx != x) {//行と列の分析との重複を防ぐ
if (sudoku[a][yy][xx] == 0) {//空欄を対象とする
for (char j = 0; j < n; j++) {
if (lst[a][y][x][j] == sudoku[a][yy][xx])lst[a][y][x][j] = 0;
//sudoku[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)]と一致する数字を
//0にすることによって候補から外す
}
}
}
}
for (char i = 0; i < n; i++) {
if (lst[a][y][x][i] > 0) {
lst[a][y][x][mx[a][y][x]] = lst[a][y][x][i];//例えば、{0, 2, 0, 4, 0, 0, 0, 0, 0}を{2, 4}と詰めて0を含めない
mx[a][y][x]++;//候補数字の個数のカウント
}
}
}
では過剰に解析がなされています。
列の動きとブロックの動きも考慮に入れて全体を見ると
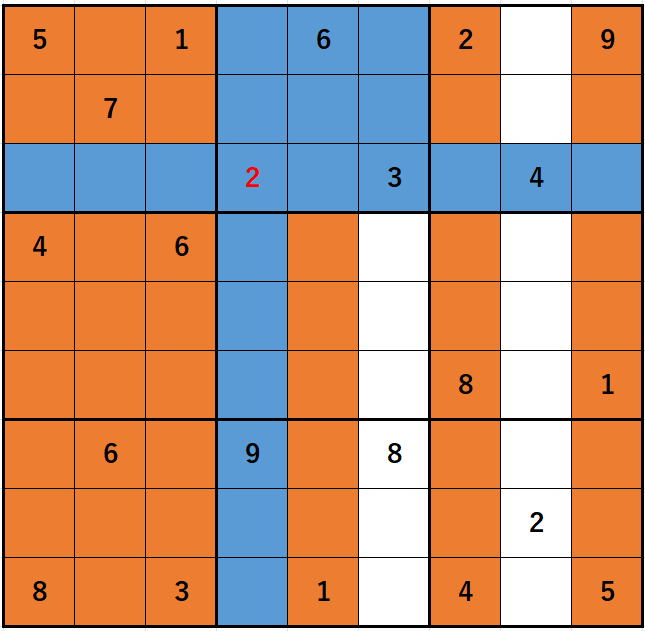（2023年11月29日訂正）となってしまうわけです。
ほとんど全体解析になってしまっています。
間違いがお分かりでしょうか。
オレンジに塗ってある空欄には何の影響を与えないので、
無意味な解析がなされています。
2 が影響を与えるのは青のみでオレンジには当然何の影響も与えません。
問題があると気付いていながら放置してきた理由は、
私の頭が混乱していたからです。
第４講第８話において主客転倒が起きているとしながら、
その後全く触れられていないのは、
私の頭が主客転倒を起こしていて混乱していたからです。
sudokukaihoにおいては他者（他のセル）への影響が考察され、
kyokusyokaisekiにおいては他者（他のセル）からの影響が考えられていて、
両者を明確に区別せずに混乱していたのです。
長い間沈黙してきた理由は、
過剰分析を解消する方法が思いつかなかったことが理由の一つです。
ですが、やっと私の頭が整理できて解析範囲を
図のように限定できました。
さあ、問題を今こそ直しましょう！
そして、関数fにおいも部分リスト解析も入れましょう。
fでもsudokukaihoでも部分解析おなじですから、
どちらかで作ってコピペしてください。
第６話へ 第８話へ
トップへ