第10話 部分解析解説
void sudokukaiho(char a, char g) {//数独を解くエンジン
・
・
・
if (keizoku == 0)return;//数独を発見したスレッドからの連絡および閉じよの指令
for (char i = 0; i < mx[a][y][x]; i++) {
char gy[n] = { 0,0,0,0,0,0,0,0,0 };
char r[n] = { 0,0,0,0,0,0,0,0,0 };
char b[n] = { 0,0,0,0,0,0,0,0,0 };
mondai[a][y][x] = lst[a][y][x][i];
//候補の数字を代入 例えば、mondai[0][1]なら{2, 4}の2，4の順に代入する
if (keizoku == 0)return;
//x[y][x]と同じ行にあるセルへの影響を調べる。
//具体的には座標(y, j)においてmondai[a][y][x]が候補数字に入っている場合には
//候補から外し、候補数字の個数も一つ減らす。
for (char j = 0; j < n; j++) {
if (j != x) {//自己を対象から外す。
if (mondai[a][y][j] == 0) {//空欄のみを解析対象にする。
for (char k = 0; k < mx[a][y][j]; k++) {
if (keizoku == 0)return;
if (mondai[a][y][x] == lst[a][y][j][k]) {
lst[a][y][j][k] = lst[a][y][j][mx[a][y][j] - 1];
lst[a][y][j][mx[a][y][j] - 1] = mondai[a][y][x];
mx[a][y][j]--;
gy[j] = 1;//座標(y, j)においてmondai[a][y][x]が候補数字から外され、
//候補数字数も減らされたことを記録している。
}
}
}
}
}
if (keizoku == 0)return;
for (char j = 0; j < n; j++) {
if (j != y) {//自己を対象から外す。
if (mondai[a][j][x] == 0) {//空欄のみを解析対象にする。
for (char k = 0; k < mx[a][j][x]; k++) {
if (keizoku == 0)return;
if (mondai[a][y][x] == lst[a][j][x][k]) {
lst[a][j][x][k] = lst[a][j][x][mx[a][j][x] - 1];
lst[a][j][x][mx[a][j][x] - 1] = mondai[a][y][x];
mx[a][j][x]--;
r[j] = 1;//座標(j, x)においてmondai[a][y][x]が候補数字から外され、
//候補数字数も減らされたことを記録している。
}
}
}
}
}
if (keizoku == 0)return;
char s = 3 * (y / 3);
char t = 3 * (x / 3);
for (char j = 0; j < n; j++) {
char yy = s + (j / 3);
char xx = t + (j % 3);
if (yy != y && xx != x) {//自己を対象から外す。
if (mondai[a][yy][xx] == 0) {//空欄のみを解析対象にする。
for (char k = 0; k < mx[a][yy][xx]; k++) {
if (keizoku == 0)return;
if (mondai[a][y][x] == lst[a][yy][xx][k]) {
lst[a][yy][xx][k] = lst[a][yy][xx][mx[a][yy][xx] - 1];
lst[a][yy][xx][mx[a][yy][xx] - 1] = mondai[a][y][x];
mx[a][yy][xx]--;
b[j] = 1;//座標(j, x)においてmondai[a][y][x]が候補数字から外され、
//候補数字数も減らされたことを記録している。
}
}
}
}
}
if (g + 1 < tm)sudokukaiho(a, g + 1);//内側部屋へ
if (cn1[a] == 2) {
return;//複数解
}
・
・
・
for (char j = 0; j < n; j++) {//以下復元作業
if (gy[j] == 1) {
mx[a][y][j]++;
}
if (r[j] == 1) {
mx[a][j][x]++;
}
if (b[j] == 1) {
char yy = 3 * (y / 3) + (j / 3);
char xx = 3 * (x / 3) + (j % 3);
mx[a][yy][xx]++;
}
}
}
}
旧方式が
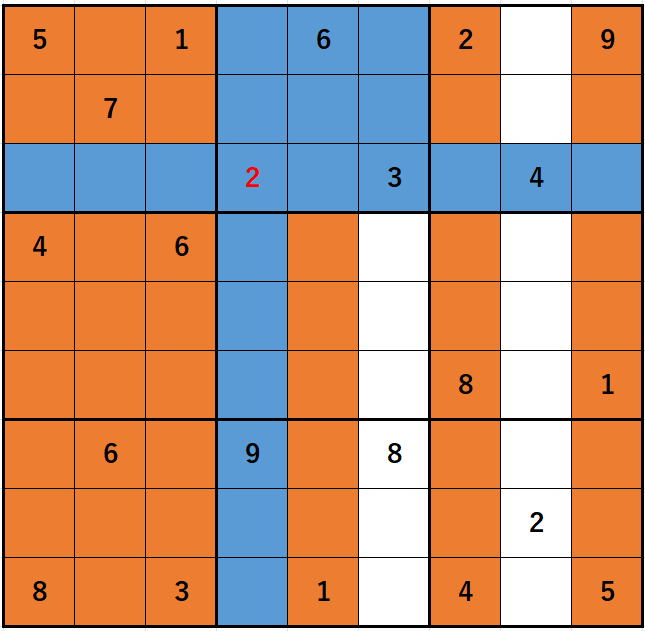
と関係ない部分まで解析してしまった理由は、
sudokukaihoの
for (int j = 0; j < n; j++)if (j != X[g])if (mondai[Y[g]][j] == 0)kyokusyokaiseki(Y[g], j);
にあります。
for (int j = 0; j < n; j++)if (j != X[g])if (mondai[Y[g]][j] == 0)の部分は
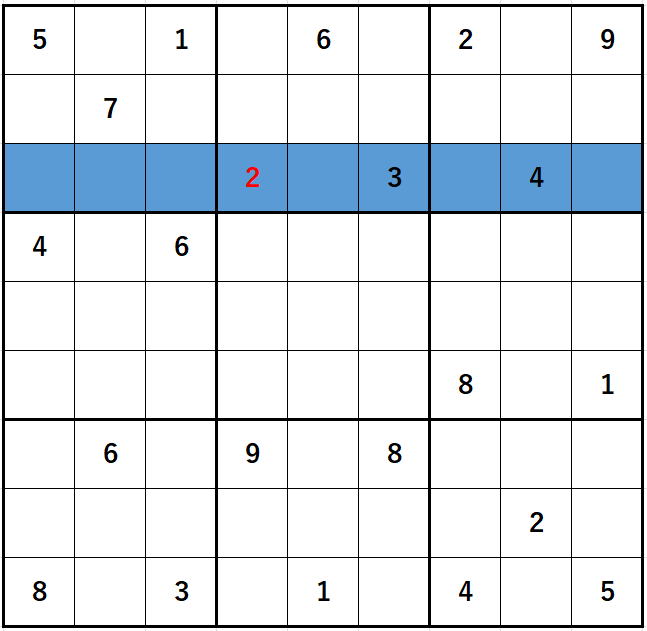（厳密には空欄のみ）と動き合っているように見えます。
問題はkyokusyokaiseki(Y[g], j);の中の
for (char i = 0; i < n; i++) {//sudoku[a][y][x]と同じ行にあるセルからの影響を調べる
if (i != x) {//自分自身は対象にしない
if (sudoku[a][y][i] > 0) {//数字が入っている欄のみを対象とする
for (char j = 0; j < n; j++) {
if (lst[a][y][x][j] == sudoku[a][y][i])lst[a][y][x][j] = 0;
//sudoku[a][y][i]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (char i = 0; i < n; i++) {//sudoku[a][y][x]と同じ列にあるセルからの影響を調べる
if (i != y) {
if (sudoku[a][i][x] > 0) {//数字が入っている欄のみを対象とする
for (char j = 0; j < n; j++) {
if (lst[a][y][x][j] == sudoku[a][i][x])lst[a][y][x][j] = 0;
//sudoku[a][i][x]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (char i = 0; i < n; i++) {//sudoku[a][y][x]と同じブロックにあるセルからの影響を調べる
char yy = 3 * (y / 3) + (i / 3);
char xx = 3 * (x / 3) + (i % 3);
if (yy != y && xx != x) {//行と列の分析との重複を防ぐ
if (sudoku[a][yy][xx] == 0) {//空欄を対象とする
for (char j = 0; j < n; j++) {
if (lst[a][y][x][j] == sudoku[a][yy][xx])lst[a][y][x][j] = 0;
//sudoku[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)]と一致する数字を
//0にすることによって候補から外す
}
}
}
}
例えば、座標（2, 0）にいるときに縦に動いていって
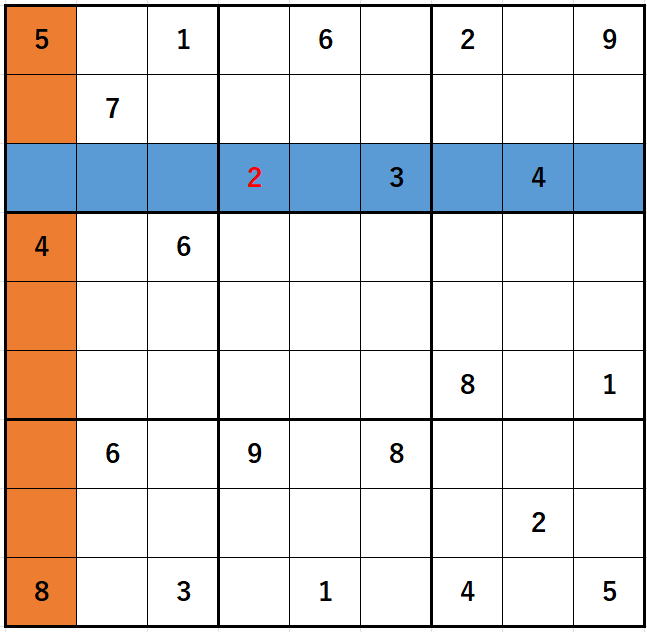
と意味のない解析をやってしまうわけです。
座標（2, 1），（2, 2），（2, 4），（2, 5），（2, 6），（2, 8）についても同様で
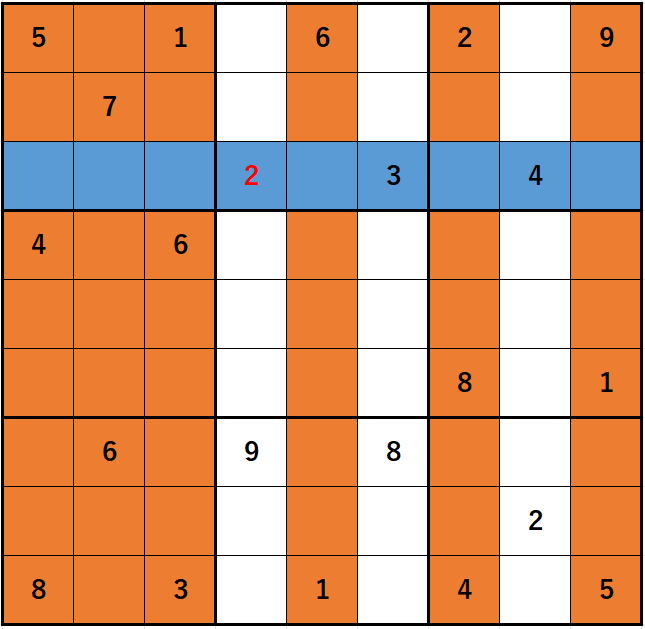
列の動きとブロックの動きも考慮に入れて全体を見ると
となってしまうわけです。
ほとんど全体解析になってしまっています。
行の動きなら
for (char j = 0; j < n; j++) {
if (j != x) {//自己を対象から外す。
if (mondai[a][y][j] == 0) {//空欄のみを解析対象にする。
for (char k = 0; k < mx[a][y][j]; k++) {
if (keizoku == 0)return;
if (mondai[a][y][x] == lst[a][y][j][k]) {
lst[a][y][j][k] = lst[a][y][j][mx[a][y][j] - 1];
lst[a][y][j][mx[a][y][j] - 1] = mondai[a][y][x];
mx[a][y][j]--;
gy[j] = 1;//座標(y, j)においてmondai[a][y][x]が候補数字から外され、
//候補数字数も減らされたことを記録している。
}
}
}
}
}
によって、
列の動きなら
for (char j = 0; j < n; j++) {
if (j != y) {//自己を対象から外す。
if (mondai[a][j][x] == 0) {//空欄のみを解析対象にする。
for (char k = 0; k < mx[a][j][x]; k++) {
if (keizoku == 0)return;
if (mondai[a][y][x] == lst[a][j][x][k]) {
lst[a][j][x][k] = lst[a][j][x][mx[a][j][x] - 1];
lst[a][j][x][mx[a][j][x] - 1] = mondai[a][y][x];
mx[a][j][x]--;
r[j] = 1;//座標(j, x)においてmondai[a][y][x]が候補数字から外され、
//候補数字数も減らされたことを記録している。
}
}
}
}
}
ブロックの動きなら
char t = 3 * (x / 3);
for (char j = 0; j < n; j++) {
char yy = s + (j / 3);
char xx = t + (j % 3);
if (yy != y && xx != x) {//自己を対象から外す。
if (mondai[a][yy][xx] == 0) {//空欄のみを解析対象にする。
for (char k = 0; k < mx[a][yy][xx]; k++) {
if (keizoku == 0)return;
if (mondai[a][y][x] == lst[a][yy][xx][k]) {
lst[a][yy][xx][k] = lst[a][yy][xx][mx[a][yy][xx] - 1];
lst[a][yy][xx][mx[a][yy][xx] - 1] = mondai[a][y][x];
mx[a][yy][xx]--;
b[j] = 1;//座標(j, x)においてmondai[a][y][x]が候補数字から外され、
//候補数字数も減らされたことを記録している。
}
}
}
}
}
によって
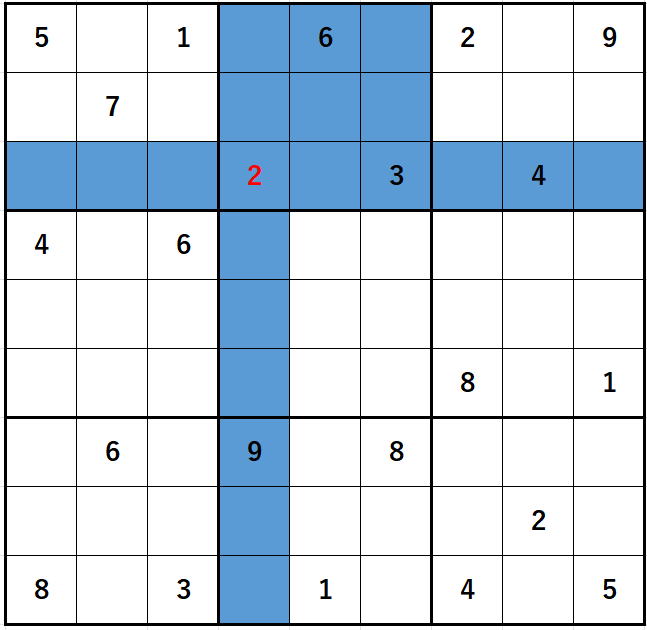
と正しい範囲の部分解析になっていて成功している様子がお分かりかと思います。
これで理詰め解法エンジン開発のための準備が終了して、
第９講から待望の理詰め解法エンジンの開発に取り組みます。
本当に永らくお待たせてしまったことをお詫び申し上げます。
その前に皆さんは第８講第６話を参考にしてソフト作りをしておきましょう。
第９話へ 第９講第１話へ
トップへ