第３話 左右対称形・上下対称形を実現するための考え方
本当にごめんなさい。
脱線で１話使ってしまいました。
線形代数学を学んでいくと、
転置行列という言葉に遭遇します。
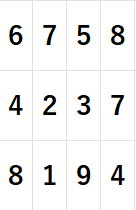
何を転置したかと申しますと、縦と横を転置したわけです。
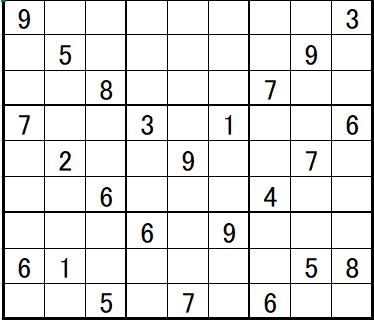
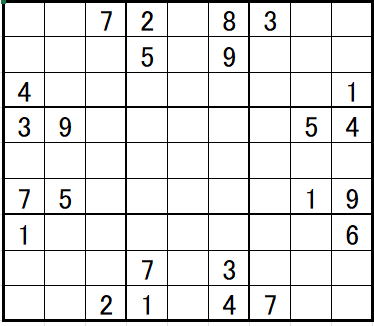
左右対称形と上下対称形はただの転置行列であり、
本質的には同じです。
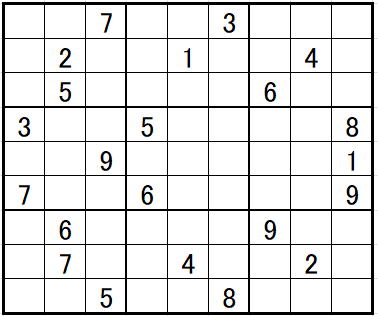
この２つの関係は縦と横を交換しただけ、
すなわち転置行列です。
つまり、どちらか一方を作って転置させればよいのです。
左右対称形から始めたいところですが、
私たちは部屋番号を上のようにつけてしまったので、
上下対称を作ってから、
転置して左右対称を作ることにしましょう。
上下対称ですから、
私たちはオレンジと青から部屋番号を選べばよいのです。
青と緑は対称だからです。
では、オレンジと青に何個ずつ入れればよいでしょうか。
青がダブルカウントでオレンジがシングルカウントです。
オレンジの個数をp、青の個数をqとすると、
２p + q = ヒント数
ということになります。
するとqすなわちオレンジの個数を決定してやればpも決まります。
qを決めるには
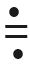は約という意味です。ひとつ重要な注を言い忘れていました。
その注とは
２p + q = ヒント数
の式から明らかなようにヒント数が奇数のときはqも奇数でなければならないということです。
例えば、ヒント数が25でq = ４ ときを考えると
２p + ４ = ２５
だと２p = ２１からp = １０.５となりpが整数であることに反してしまいます。
オレンジの部分の冒頭は次のようにするとよいと思います。
char c[3];
if (hnt % 2 == 0) {
for (char i = 0; i < 3; i++)c[i] = 2 * i;
}
if (hnt % 2 == 1) {
for (char i = 0; i < 3; i++)c[i] = 2 * i + 1;
}
char q = c[rand() % 3];
本当は平均が hnt / 9 になるようにしたいところですが、
上の案では平均は偶数の場合が２で、奇数の場合が３です。
ヒント数24ならhnt / 9 = 2 ヒント数25ならhnt / 9 = 3 ですから私はこれで妥協しました。
皆さんは是非、いかなるヒント数でも平均がほぼ同じようになるように工夫してください。
では皆さん上下に対称と左右に対称のプログラムに挑戦してください。
それから、
void f(char a, char s) {//ヒント数0の数独を解く関数
・
・
・
for (char i = 0; i < n; i++) {
sudoku[a][y][x] = e[(i + ii) % n]; //２次元配列に１から９までの整数を入力
・
・
・
if (s == n * n - 1) { //一番奥に部屋に到達
char hb; //部屋番号
char tbs[13] = { 11,13,17,19,23,29,31,37,41,43,47,53,59 }; //飛びの選択肢
//素数であれば81と互いに素は保証されている
char st = rand() % 81; //始めの位置
char tb = tbs[rand() % 13]; //飛び
char h = 0; //可否の否
char* gohr = (char*)calloc(hnt, sizeof(char));
for (char t = 0; t < hnt; t++) {
gohr[t] = (st + t * tb) % 81;
}
for (char j = 0; j < n; j++) {
for (char k = 0; k < n; k++) {
if (keizoku == 0)return;
hb = n * j + k; //部屋番号の再初期化 = 空欄の数字候補の個数の小さい順に入れる
char h = 0; //可否の否
for (char t = 0; t < hnt; t++) {
if (gohr[t] == hb) {
h = 1;//可否の可
break;
}
}
if (h == 1) {
mondai[a][j][k] = sudoku[a][j][k]; //問題用の配列に代入
gensudoku[a][j][k] = sudoku[a][j][k];
}
}
}
・
・
・
tobi:;
}
}
の青色部分は大きすぎますので、
この機会に関数として独立させましょう。
つまり、非対称を含めて①非対称②左右対称③上下対称④左右にも上下にも対称⑤ハート型と
問題配置の関数として５個できることになります。
if (s == n * n - 1) { //一番奥に部屋に到達
int k = rand() % 3;
if (k == 0)hitaisyou(a);
if (k == 1)sayutaisyou(a);
if (k == 2)jyogehitaisyou(a);
cn[a]++;
return; //数独が1個できた時点でとめる 2023年11月29訂正
}
}
tobi:;
}
}
void hitaisyou(char a) {
char hb; //部屋番号
char tbs[13] = { 11,13,17,19,23,29,31,37,41,43,47,53,59 }; //飛びの選択肢
//素数であれば81と互いに素は保証されている
char st = rand() % 81; //始めの位置
char tb = tbs[rand() % 13]; //飛び
char h = 0; //可否の否
char* gohr = (char*)calloc(hnt, sizeof(char));
for (char t = 0; t < hnt; t++) {
gohr[t] = (st + t * tb) % 81;
}
for (char j = 0; j < n; j++) {
for (char k = 0; k < n; k++) {
if (keizoku == 0)return;
hb = n * j + k; //部屋番号の再初期化 = 空欄の数字候補の個数の小さい順に入れる
char h = 0; //可否の否
for (char t = 0; t < hnt; t++) {
if (gohr[t] == hb) {
h = 1;//可否の可
break;
}
}
if (h == 1) {
mondai[a][j][k] = sudoku[a][j][k]; //問題用の配列に代入
gensudoku[a][j][k] = sudoku[a][j][k];
}
}
}
free(gohr); //メモリ解放
}
void sayutaisyou(char a) {
}
void jyogehitaisyou(char a) {
}
では皆さん上下に対称と左右に対称のプログラムに挑戦してください。
第２話へ 第４話へ
トップへ