第2話 よもやま話



まず、左右対称形から出発しましょうと、
言いたいところですが、実は上下対称形と左右対称形は本質的には同じです。
行と列を交換した行列を転置行列と言います。
そうすると行列って何よ?という声を心の中で発している人もいるでしょう。
ですよね。
高校までの数学では行列を学ばないからです。
正確には本格的には学ばないからと言わなければなりませんね。
数Bをとると少しだけ学びます。
行列の例を挙げると・・・・
答えは20行下に
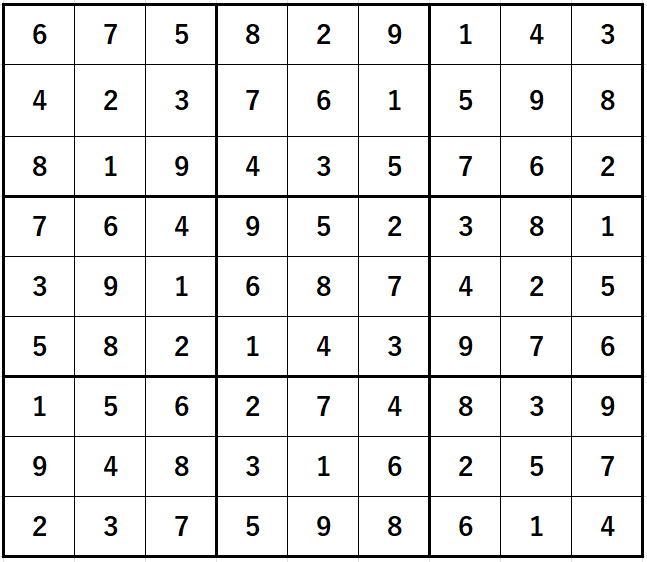
なんだ?それって今までさんざん作ってきた数独の解答ではないか!
と皆さんは思いましたよね。
そうです。
解答だけでなく
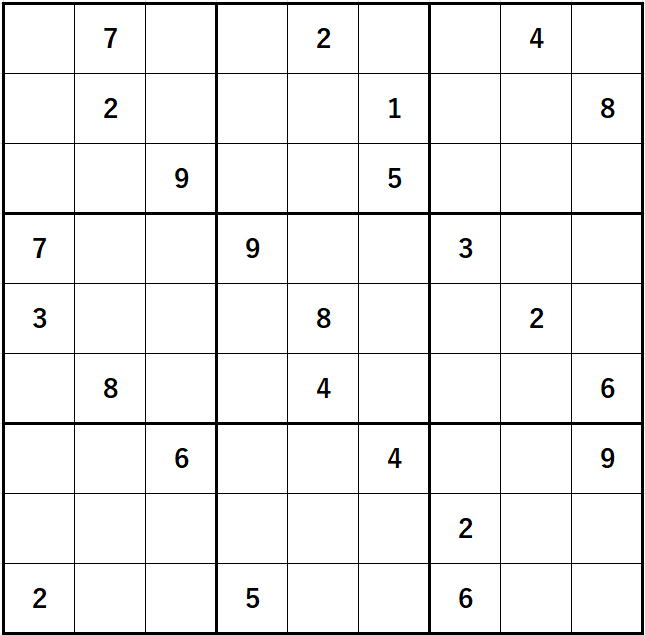
空白セルを0と解釈すればこれも行列の一つです。
ですから、今まで作ってきたナンプレはすべて行列なのです。
そして、行数(横列数)と列数(縦列数)が同数の行列を正方行列と言います。
私が日常生活では使わない呼称である行(横列のこと)にこだわるのは線形代数学を学んだからです。
東大から引き抜かれてきた新進気鋭の数学者(飯高茂先生=代数幾何学の世界的権威)が
線形代数学の問題を出題され、
複素関数論をつかってその宿題に2行で解答を与えた私の解法を
新進気鋭の数学者は絶賛して私には全く思いつかなかった天才的な方法であり、
この解法を思いついた学生は間違いなく天才であると言ってくださったのです。
学生から提出されたレポートには解法は大きく分けて5つがあり、
他の4つの解法ではレポート用紙で3枚から4枚も計算していかないと、
解答にたどり着けないのに2行で答えに至ったことに驚嘆したわけです。
ついでに言いますと、その学生のレポートにはそれとは異なる解法が3つ示されていた、
と褒められたのです。
私が線形代数学とは根本から異なる複素関数論を使って解いたのには、
仕掛けがあります。
それは、中3の時にド・モアブルの公式を布団
の中(私はよく布団に入ってからいろいろ考える悪しき習慣がありました)
で発見したことが余りにも強烈すぎて、思わず体を起こしたほどです。
大変偉大な発見をしたと思ったのです。
私は、本を読む習慣がまったくなかったので完全に独力で発見したわけです。
おなじくネピアの対数を中2のときに独力で発見しています。
もちろん、中学3年生ですから当時は高校2年生でド・モアブルの公式を習うということは知りませんでした。
いかなる問題にもド・モアブルの公式を使って簡単に解けないか、
ということを常に試してみるという習慣が身についていただけだったのです。
ですから、飯高茂先生には申し訳ありませんが私は天才ではありません。
ごめんなさい。脱線魔なのです。話を元に戻しましょう。行数と列数が異なる長方形上に並んでいる
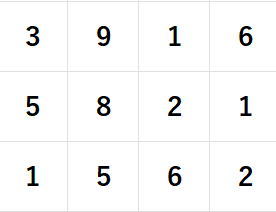
も行列の一つです。ただし、厳密には左右に()ないしは[ ]がつきます。
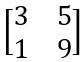
理系学部に進むと線形代数学という学問が必修のために、
理系に進んだ方は全員が線形代数学を学ぶことになるのですが、
特に、物理学科や化学科に進んだ人たちにとってはきわめて重要な必修学問ということになります。
今量子力学の性質を生かした量子コンピュータの話題が流行っていますが、
その量子力学においても行列の知識は必須のツールです。
20世紀初頭から今までのニュートン力学やマックウェルの電磁気学では、
説明できない現象が見つかりニュートン力学で万物が説明できるわけではないことを
認めなければならなくなります。
そして、
1920年代になると古典力学(ニュートン力学)では説明できない諸現象を統一的に説明できる
体系が2つ現れます。
シュレーディンガーの波動力学とハイゼンベルグの行列力学です。
2つの体系は見かけも全く異なり使う数学も異なります。
波動力学では偏微分方程式を使い、行列力学では名前の通り行列(線形代数学)を使います。
それなのに両体系が導き出す結論はことごとく一致しました。
どちらの理論が正しいのか理論物理学者の間で論争が起きます。
それに決着をつけた物理学者はシュレーディンガー自身です。
シュレーディンガーは両体系が数学的には同値であることを証明しました。
こうして量子力学という学問が成立したのです。
そして、Googleの量子コンピュータが
2019年に量子超越(量子コンピュータがスーパーコンピュータの性能を上回ること)を起こし、
世界最速のスパコンをもってしても2万年かかる計算を200秒で計算したのです。
ただし、これはGoogleの主張であってIBMは2万年は誇張でせいぜい2,3日というところだと批判しています。
仮に2日だとしても2 × 24 × 3600 ÷ 200 = 864倍の速度を実現しているので、
量子超越は実現しているといってよいと思います。
現在では400量子ビットぐらいですが、
近い将来100万量子ビットの量子コンピュータが実用化され、
製薬や蓄電池の研究が飛躍的に発展するだろうと言われています。
ワクワクする時代になりました。
市場規模はなんと110兆円だそうです。
第1話へ 第3話へ
トップへ