第６講 残された課題の解消とマルチスレッド化
第３話 唯一解または複数解の判定と数独作成時間・数独解法時間の表示
唯一解または複数解を確認するのも、数独作成時間と数独解法時間を表示させるのも大変簡単です。


unsigned u = (unsigned)time(NULL);
//マルチスレッド化した際にルートスレッドと
//発生させたスレッドに共有させるためにグローバル変数に変更
int main() {
　　clock_t hj, ow;
　　hj = clock();
　　syokika();
　　srand(u); //シード整数値を現在の起動時の時刻から取得
　　f(0);
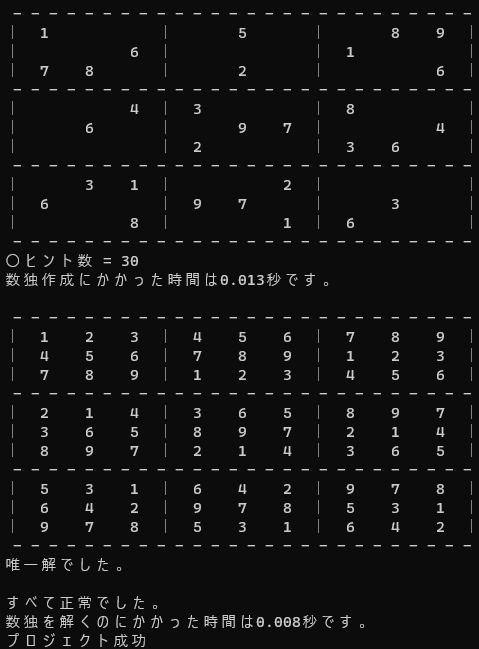
　　cout << "ヒント数 = " << hnt << endl;
　　ow = clock();
　　cout << "数独作成にかかった時間は" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl << endl;
　　hj = clock();
　　for (int i = 0; i < n; i++) {
　　　　for (int j = 0; j < n; j++) {
　　　　　　if (mondai[i][j] == 0)kyokusyokaiseki(i, j);
　　　　　　//セルリスト構造解析 = 単セル解析を積み重ねれば全体構造解析になる
　　　　}
　　}
　　sudokukaiho(hnt);//数独を解くエンジン 部分構造解析を進めながら問題を解いていく
　　if (cn1 == 1)cout << "唯一解でした。" << endl;
　　if (cn1 == 2)cout << "解が少なくとも２個存在します。" << endl;
　　ow = clock();
　　if (sng == 1)cout << endl << "すべて正常でした。" << endl;
　　cout << "数独を解くのにかかった時間は" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl;
　　cout << "プロジェクト成功" << endl;
　　while (!_kbhit()); //待機させるための命令
　　return(0);
}
　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　・
void sudokukaiho(int g) {//数独を解くエンジン
　　nextcell(g);//座標(Y[g], X[g])の取得
　　for (int i = 0; i < mx[Y[g]][X[g]]; i++) {
　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　・
　　　　if (g + 1 < tm)sudokukaiho(g + 1);//内側部屋へ
　　　　if (cn1 == 2) {
　　　　　　return;//複数解または唯一解を証明する
　　　　}
　　　　if (g == tm - 1) {
　　　　　　hy();//解答表示
　　　　　　cn1++;
　　　　}
　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　・
さて、残された課題が解消されて次話でいよいよマルチスレッド化に挑戦します。

マルチスレッド化するために皆さんにやっていただきたいことがあります。

マルチスレッドにすると結構メモリを食いますのでint型をchar型に一気に変換して頂きたいのです。

ただし、表示部分に問題が出ますので

hntを+hntに


のmondai[i][j]を+mondai[i][j]に変更してください。

char型を使って表示させる場合は+を冒頭につける必要があります。

テキストファイル

もしうまくいかない場合は上のテキストファイルをコピペしてください。

int型をchar型に変更した時の実行画面


ごめんなさい。

もう一つやらなければならないことがありました。それは、

③複数解ときは探索を継続して唯一解が見つかったら表示させる

という課題です。

この課題に取り組む際に
#include<iostream>
#include<conio.h> //while (!_kbhit())を使うために必要
#include <process.h> /* _beginthread, _endthread　を使うために必要　マルチスレッド化に必要 */
using namespace std;
void f(char a, char s); //sは次元番号=部屋番号
const char n = 9; //16次数独や25次数独も考えてnと一般化した。
const char th = 30;
const char hnt = 40;
const char tm = 81;
char cn = 0; //順列を数える変数
char cn1 = 0; //順列を数える変数
char sudoku[th][n][n]; //解答用２次元配列（魔方陣の研究から始まったので本体をmとしてきた。
char mondai[th][n][n]; //mondai[th][n][n]は解答用であるが、問題を解くとsudoku[th][n][n]と同じになってしまう
char gensudoku[th][n][n];//これが真の解答
char sng = 1;//１ならば真
void syokika(char a);
void hy(char a);//結果をコンソール画面に表示する関数
void kyokusyokaiseki(char a,char y, char x);//単セル解析（候補数字探索）
void nextcell(char a, char g);//次に入力するセルを探索する関数
void sudokukaiho(char a, char g);//数独を解くエンジン 部分構造解析を進めながら問題を解いていく
void hontai(void* a);
char lst[th][n][n][n];//セルリスト構造解析によって可能な数字を収容する３次元配列
char mx[th][n][n];//セルの数字候補の個数
char Y[th][n * n], X[th][n * n];//次に入力するセルのy座標とx座標
unsigned u = (unsigned)time(NULL);
//マルチスレッド化した際に、
//ルートスレッドと発生させたスレッドが共有できるようにグローバル変数に変更
char keizoku = 1;
clock_t hj0[th], ow0[th], hj1[th], ow1[th];
char main() {

9は先ほどの置換を利用してnに変更し、

定数類はなるべく上に置くということで、

#include<iostream>
#include<conio.h> //while (!_kbhit())を使うために必要
#include <process.h> /* _beginthread, _endthread　を使うために必要　マルチスレッド化に必要 */
using namespace std;
void f(char a, char s); //sは次元番号=部屋番号
const char n = 9; //16次数独や25次数独も考えてnと一般化した。
const char th = 30;
const char hnt = 40;
const char tm = 81;
としました。

それから
void f(int s) {//ヒント数0の数独を解く関数
　　　　　　　　　　　　・
　　　　　　　　　　　　・
　　　　　　　　　　　　・
　　　　if (s == n * n - 1) { //一番奥に部屋に到達
　　　　　　int hb; //部屋番号
　　　　　　　　　　　　・
　　　　　　　　　　　　・
　　　　　　　　　　　　・
　　　　　　hy();//問題表示
　　　　　　free(gohr); //メモリ解放
　　　　　　int p[9];//重複検査のための配列
　　　　　　int kr;
　　　　　　for (int j = 0; j < n; j++) {
　　　　　　　　for (int k = 0; k < n; k++)p[k] = 0;//初期化
　　　　　　　　　　kr = 1; //初期化
　　　　　　　　　　for (int k = 0; k < n; k++) {
　　　　　　　　　　　　p[sudoku[j][k] - 1] = 1;
　　　　　　　　　　}
　　　　　　　　　　for (int k = 0; k < n; k++) {
　　　　　　　　　　　　if (p[k] == 0) { //行の重複検査
　　　　　　　　　　　　cout << "×";
　　　　　　　　　　　　kr = 0;
　　　　　　　　　　　　sng = 0;
　　　　　　　　　　　　goto tobi1;
　　　　　　　　　　}
　　　　　　　　}
　　　　　　　　for (int k = 0; k < n; k++)p[k] = 0;//初期化
　　　　　　　　kr = 1; //初期化
　　　　　　　　for (int k = 0; k < n; k++) {
　　　　　　　　　　p[sudoku[k][j] - 1] = 1;
　　　　　　　　}
　　　　　　　　for (int k = 0; k < n; k++) {
　　　　　　　　　　if (p[k] == 0) { //列の重複検査
　　　　　　　　　　　　cout << "×";
　　　　　　　　　　　　kr = 0;
　　　　　　　　　　　　sng = 0;
　　　　　　　　　　　　goto tobi1;
　　　　　　　　　　}
　　　　　　　　}
　　　　　　　　for (int k = 0; k < n; k++)p[k] = 0;//初期化
　　　　　　　　kr = 1; //初期化
　　　　　　　　for (int k = 0; k < n; k++) {
　　　　　　　　　　p[sudoku[3 * (j / 3) + (k / 3)][3 * (j % 3) + (k % 3)] - 1] = 1;
　　　　　　　　}
　　　　　　　　for (int k = 0; k < n; k++) {
　　　　　　　　　　if (p[k] == 0) {//ブロックの重複検査
　　　　　　　　　　　　cout << "×";
　　　　　　　　　　　　kr = 0;
　　　　　　　　　　　　sng = 0;
　　　　　　　　　　　　goto tobi1;
　　　　　　　　　　}
　　　　　　　　}
　　　　　　}
　　　tobi1:;
　　　　　　if (kr == 1)cout << "〇";
　　　　　　cn++;
　　　　　　if (cn == 1)return; //数独が1個できた時点でとめる
　　　　}
　　tobi:;
　　}
}
数独を解いて唯一解であることがわかっていますから、

青は不要ですから削除してください。

③複数解ときは探索を継続して唯一解が見つかったら表示させる

を実現できればシングルスレッド版の数独自動生成ソフトが完成したことになります。

シングル数独自動生成ソフトの実行画面

別解がないように改良するわけですから、

数独自動生成ソフトが完成といってもよいと思います。

ヒント数が40もあるので仮定法＝背理法＝試行錯誤法を使わなければ解けない数独を

生成する可能性はほぼ 0 だと思います。

つまり、理詰めで解ける数独のみを生成する数独自動生成ソフトの開発にほぼ成功したことになります。

第２話へ　第４話へ

トップへ