第６講 残された課題の解消とマルチスレッド化
第２話 ランダムの度合いをあげて問題を解いている方が傾向を予想できないようにする

の実現
u = (unsigned)time(NULL);//他の関数でも共有するためにグーバル変数に変更
int main() {
　　clock_t hj, ow;
　　hj = clock();
　　syokika();
　　f(0);
　　cout << "ヒント数 = " << hnt << endl;
　　for (int i = 0; i < n; i++) {
　　　　for (int j = 0; j < n; j++) {
　　　　　　if (mondai[i][j] == 0)kyokusyokaiseki(i, j);
　　　　　　//セルリスト構造解析 = 単セル解析を積み重ねれば全体構造解析になる
　　　　}
　　}
　　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　　・
void f(int s) {//ヒント数0の数独を解く関数
　　int y = s / 9; //縦座標
　　int x = s % 9; //横座標
　　//srand(u); //シード整数値を現在の時刻から取得　後に2はuに戻す
　　int e[9];
　　e[0] = rand() % 9 + 1;
　　int i = 1;
　　while (i < 9) {
　　　　e[i] = rand() % 9 + 1;
　　　　while (1) {
　　　　　　int h = 1;
　　　　　　e[i] = rand() % 9 + 1;
　　　　　　for (int j = 0; j < i; j++) {
　　　　　　　　if (e[i] == e[j]) {
　　　　　　　　　　h = 0;
　　　　　　　　　　break;
　　　　　　　　}
　　　　　　}
　　　　　　if (h == 1)break;
　　　　}
　　　　i++;
　　}
　　int ii = rand() % 9; //始まりをランダムにする
　　for (int i = 0; i < n; i++) {
　　　　sudoku[y][x] = e[(i + ii) % n]; //２次元配列に１から９までの整数を入力

　　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　　・

うまくいっているのかを確証するプログラム全文
#include<iostream>
#include<conio.h> //while (!_kbhit())を使うために必要
using namespace std;
int main() {
　　unsigned u = (unsigned)time(NULL);
　　srand(u);
　　int e[9];
　　e[0] = rand() % 9 + 1;
　　int i = 1;
　　while (i < 9) {
　　　　e[i] = rand() % 9 + 1;
　　　　while (1) {
　　　　　　int h = 1;
　　　　　　e[i] = rand() % 9 + 1;
　　　　　　for (int j = 0; j < i; j++) {
　　　　　　　　if (e[i] == e[j]) {
　　　　　　　　　　h = 0;
　　　　　　　　　　break;
　　　　　　　　}
　　　　　　}
　　　　　　if (h == 1)break;
　　　　}
　　　　i++;
　　}
　　for (int i = 0; i < 9; i++)cout << e[i] << " ";
　　cout << endl;
　　cout << "プロジェクト終了" << endl;
}
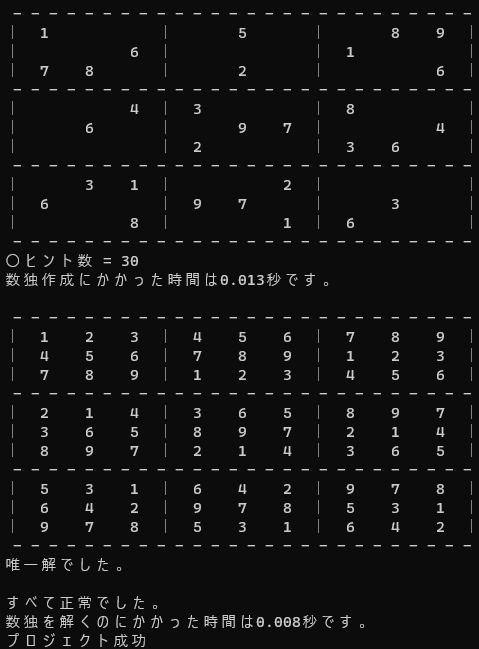
実行画面





ランダム度は明確に上がっています。

しかもこの順で実行するのではなくて、
　　int ii = rand() % 9; //始まりをランダムにする
　　for (int i = 0; i < n; i++) {
　　　　sudoku[y][x] = e[(i + ii) % n]; //２次元配列に１から９までの整数を入力
　　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　　・
例えば、e[9]が3，6，1，7，9，5，8，4でiiが4だとすれば

9，5，8，4，3，6，1，7の順に実行されます。

２重ランダムにすることによってランダムの度合いを上げたわけです。

残された最後の課題は、唯一解の証明です。

皆さん考えてください。

その改良を加える際に数独作成時間と数独解法時間を計測してそれぞれの時間を

画面に出力するように変更してください。


マルチスレッド化するために
void f(int s) {//ヒント数0の数独を解く関数
　　int y = s / 9; //縦座標
　　int x = s % 9; //横座標
　　unsigned u = (unsigned)time(NULL);
　　srand(u); //シード整数値を現在の時刻から取得　
の青の２行はそれぞれ下記のように移動させてください。
unsigned u = (unsigned)time(NULL);
//マルチスレッド化した際にルートスレッドと
//発生させたスレッドに共有させるためにグローバル変数に変更
int main() {
　　clock_t hj, ow;
　　hj = clock();
　　syokika();
　　srand(u); //シード整数値を現在の起動時の時刻から取得　
　　f(0);

第１話へ　第３話へ

トップへ