第2話 Ⅰ.単セル解析(候補数字探索)で行った部分解析はなぜ逆部分解析を必要としないのか①
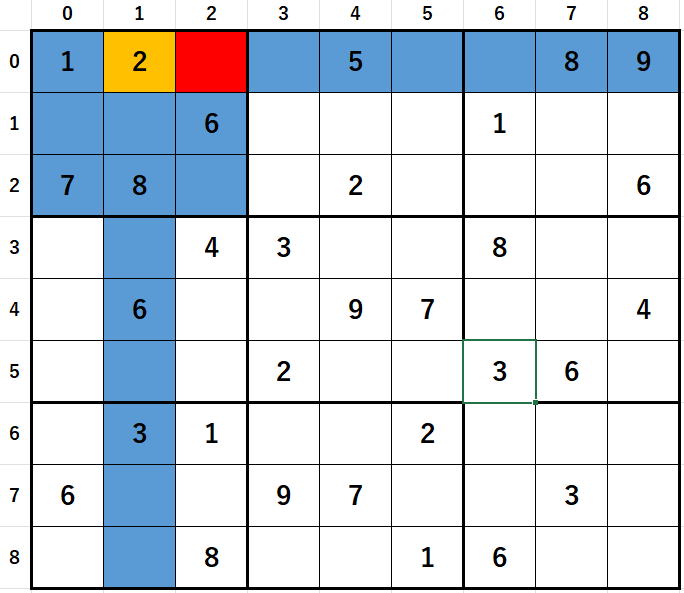
オレンジの2が放射性物質でその放射性物質が放つ放射線は上のすべての青に届きます。
その結果セルの候補数字に2があった場合に青のセルの候補数字から2が外され、
さらに候補数字数も1つ減らされます。
なんだ、結局放射線の影響を受けるのはオレンジのセルではなく他者ではないか?
それなのに現在地である座標(0,1)で今仕事をしている
void sudokukaiho(int g) {//数独を解くエンジン
nextcell(g);//座標(Y[g], X[g])の取得
for (int i = 0; i < mx[Y[g]][X[g]]; i++) {
mondai[Y[g]][X[g]] = lst[Y[g]][X[g]][i];
//候補の数字を代入 例えば、mondai[0][1]なら{2, 4}の2,4の順に代入する
for (int j = 0; j < n; j++)if (j != X[g])if (mondai[Y[g]][j] == 0)kyokusyokaiseki(Y[g], j);
//x[Y[g]][X[g]]と同じ行にあるセルの単セル解析(候補数字探索)
for (int j = 0; j < n; j++)if (j != Y[g])if (mondai[j][X[g]] == 0)kyokusyokaiseki(j, X[g]);
//x[Y[g]][X[g]]と同じ列にあるセルの単セル解析(候補数字探索)
int s = 3 * (Y[g] / 3);
int t = 3 * (X[g] / 3);
for (int j = 0; j < n; j++) {
if (s + (j / 3) != Y[g] && t + (j % 3) != X[g]) {//行解析と列解析と重複させないため
if (mondai[s + (j / 3)][t + (j % 3)] == 0) {
kyokusyokaiseki(s + (j / 3), t + (j % 3));
//x[Y[g]][X[g]]と同じブロックにあるセルの単セル解析(候補数字探索)
}
}
}
if (g + 1 < tm)sudokukaiho(g + 1);//内側部屋へ
if (cn1 == 1) {
return;//1つで来た時点で止める
}
if (g == tm - 1) {
hy();//解答表示
cn1 = 1;
}
if (i == mx[Y[g]][X[g]] - 1) {
//i < mx[Y[g]][X[g]] - 1)のときはiが1つ進んで上で単セル解析(候補数字探索)を行うので
//キャンセルは不要だが、最後だけはキャンセルをしなければならないので単セル解析(候補数字探索)
//を行う必要がある
//cout << "*-*-*-*-復元-*-*-*-*-*" << endl;
mondai[Y[g]][X[g]] = 0;
//cout << g << endl;
for (int j = 0; j < n; j++)if (j != X[g])if (mondai[Y[g]][j] == 0)kyokusyokaiseki(Y[g], j);
for (int j = 0; j < n; j++)if (j != Y[g])if (mondai[j][X[g]] == 0)kyokusyokaiseki(j, X[g]);
for (int j = 0; j < n; j++) {
if (s + (j / 3) != Y[g] && t + (j % 3) != X[g]) {
if (mondai[s + (j / 3)][t + (j % 3)] == 0) {
kyokusyokaiseki(s + (j / 3), t + (j % 3));
}
}
}
}
}
}
sudokukaihoは放射性物質まき散らして放射能汚染をもたらせたのだから、
責任をもって放射能汚染を除染してから i を1つ進める必要があるはずだと思う方は、
慧眼な方です。
ですが、除染が必要なのはif (i == mx[Y[g]][X[g]] - 1) のときだけです。
もちろん、放射能汚染や除染などは比喩です。
正確に言うと部分構造解析と逆部分構造解析です。
なぜ i < mx[Y[g]][X[g]] - 1 ときは部分構造解析のキャンセル=逆部分構造解析が必要がないのでしょうか。
その秘密は『・?・?・?』
知りたい方は第3話へGo!
第1話へ 第3話へ
トップへ