第1話 第4講で完成させたプログラムコードの謎

主要部分再掲
void sudokukaiho(int g) {//数独を解くエンジン
nextcell(g);//座標(Y[g], X[g])の取得
for (int i = 0; i < mx[Y[g]][X[g]]; i++) {
mondai[Y[g]][X[g]] = lst[Y[g]][X[g]][i];
//候補の数字を代入 例えば、mondai[0][1]なら{2, 4}の2,4の順に代入する
for (int j = 0; j < n; j++)if (j != X[g])if (mondai[Y[g]][j] == 0)kyokusyokaiseki(Y[g], j);
//x[Y[g]][X[g]]と同じ行にあるセルの単セル解析(候補数字探索)
for (int j = 0; j < n; j++)if (j != Y[g])if (mondai[j][X[g]] == 0)kyokusyokaiseki(j, X[g]);
//x[Y[g]][X[g]]と同じ列にあるセルの単セル解析(候補数字探索)
int s = 3 * (Y[g] / 3);
int t = 3 * (X[g] / 3);
for (int j = 0; j < n; j++) {
if (s + (j / 3) != Y[g] && t + (j % 3) != X[g]) {//行解析と列解析と重複させないため
if (mondai[s + (j / 3)][t + (j % 3)] == 0) {
kyokusyokaiseki(s + (j / 3), t + (j % 3));
//x[Y[g]][X[g]]と同じブロックにあるセルの単セル解析(候補数字探索)
}
}
}
if (g + 1 < tm)sudokukaiho(g + 1);//内側部屋へ
if (cn1 == 1) {
return;//1つで来た時点で止める
}
if (g == tm - 1) {
hy();//解答表示
cn1 = 1;
}
if (i == mx[Y[g]][X[g]] - 1) {
//i < mx[Y[g]][X[g]] - 1)のときはiが1つ進んで上で単セル解析(候補数字探索)を行うので
//キャンセルは不要だが、最後だけはキャンセルをしなければならないので単セル解析(候補数字探索)
//を行う必要がある
//cout << "*-*-*-*-復元-*-*-*-*-*" << endl;
mondai[Y[g]][X[g]] = 0;
//cout << g << endl;
for (int j = 0; j < n; j++)if (j != X[g])if (mondai[Y[g]][j] == 0)kyokusyokaiseki(Y[g], j);
for (int j = 0; j < n; j++)if (j != Y[g])if (mondai[j][X[g]] == 0)kyokusyokaiseki(j, X[g]);
for (int j = 0; j < n; j++) {
if (s + (j / 3) != Y[g] && t + (j % 3) != X[g]) {
if (mondai[s + (j / 3)][t + (j % 3)] == 0) {
kyokusyokaiseki(s + (j / 3), t + (j % 3));
}
}
}
}
}
}
用語の簡略化について
今までこだわりがあり、全体構造解析・部分構造解析・セルリスト構造解析など構造をつけてきましたが、
読者の皆さんからするとわかりにくい言葉であると考え、基本構造という言葉をこれからはカットしていきます。
ただ、気まぐれな性格なので構造が入ってしまう場合もあると思います。
Ⅰ.単セル解析(候補数字探索)で行った部分解析はなぜ逆部分解析を必要としないのか。
単セル解析を繰り返していけば、部分解析または全体解析になることは第4講第8話で説明してあります。
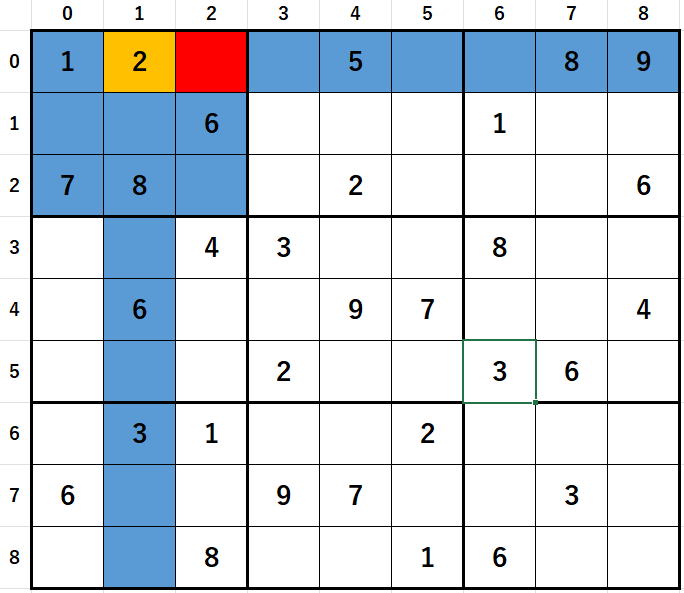
なぜなら、赤などのセルの解析をやっていけば青の解析すなわり部分解析になるのです。
(0,2),(0,3),(0,5),(0,6),(1,1),(1,3),(1,5),(1,7),(1,8),(1,0),(1,5),(2,2)
の解析をすれば
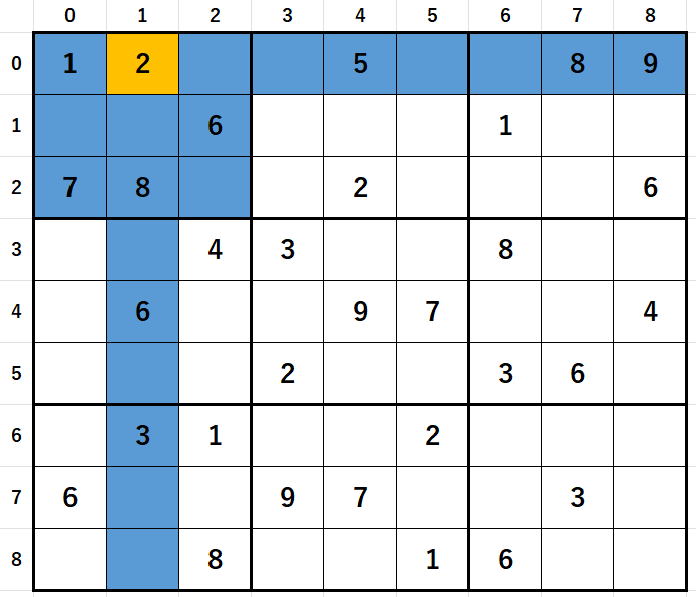
部分解析となります。部分とは空欄の青の総計を言っているわけです。
ここでは明らかにオレンジのセル(0,1)に2を代入したことによる周りに与える影響を考えています。
ですから、オレンジが主体(店主)で青は客体(お客さん)です。
不適切な例ですが、放射線を被爆する人は客体(被害者=お客さん)で
主体(主人公)は放射性物質が放射する放射線です。
オレンジが影響を与え、青は影響を受けるのです。
具体的には青のセルに数字候補2が入っている場合には影響を受ける側が2を候補から外すわけです。
周りに与える影響を考慮するのが部分解析です。
分析されているのはオレンジの周りです。

ですが、ご主人様については何の分析もしていません。
ときの主体が現在分析対象になっているのに、
周りへの影響を考察しているだけなのはおかしくないでしょうか。
いま「ときの」を使ったばかりですが、人によっては「時の」と書きます。
全く関係ない話のように見えますが、実は結論の示唆です。
そうです。答えは『時』にあります。
意味ありげな放射線の例えも、まさに結論の暗示です。
すみません。用事があり出かけなければなりませんので、今日はここで終了します。
問だけ出して逃げるなんて「ありえない」と思っていらっしゃいますよね。
ごめんなさい。今日帰ってきてから必ず続きを書きますので、許してください。
第4講第9話へ 第2話へ
トップへ