第10話 試行錯誤法第２案
もし、下をコピペするとエラーする場合は
テキストファイルをコピペしてください。
#include<iostream>
#include<conio.h> //while (!_kbhit())を使うために必要
using namespace std;
void f(int s); //sは次元番号=部屋番号
const int n = 9; //16次数独や25次数独も考えてnと一般化した。
int cn = 0; //順列を数える変数
int cn1 = 0; //順列を数える変数
int sudoku[n][n]; //解答用２次元配列（魔方陣の研究から始まったので本体をmとしてきた。
int mondai[n][n]; //sudoku[n][n]は解答用なので、問題用の２次元配列を用意した。
int sng = 1;//１ならば真
const int hnt = 30;
const int tm = 81;
void syokika();
void hy();//結果をコンソール画面に表示する関数
void cellslstkaiseki();//全体構造解析 = 全セルリスト構造解析
void nextcell(int g);//次に入力するセルを探索する関数
void sudokukaiho(int g);//数独を解くエンジン 部分構造解析を進めながら問題を解いていく
int lst[9][9][9];//セルリスト構造解析によって可能な数字を収容する３次元配列
int mx[9][9];//セルの数字候補の個数
int Y[81], X[81];//次に入力するセルのy座標とx座標
int main() {
clock_t hj, ow;
syokika();
f(0);
hj = clock();
cout << "ヒント数 = " << hnt << endl;
cellslstkaiseki();//全体構造解析 = 全セルリスト構造解析
sudokukaiho(hnt);//数独を解くエンジン 部分構造解析を進めながら問題を解いていく
ow = clock();
if (sng == 1)cout << endl << "すべて正常でした。" << endl;
cout << "計算時間は" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl;
cout << "プロジェクト成功" << endl;
while (!_kbhit()); //待機させるための命令
return(0);
}
void syokika() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
sudoku[i][j] = 0;
mondai[i][j] = 0;
}
}
}
void hy() {
for (int i = 0; i < 26; i++)cout << " -"; //最初の横線
cout << endl;
for (int i = 0; i < n; i++) {
cout << "｜";//最初の縦線
for (int j = 0; j < n; j++) {
if (mondai[i][j] > 0) {
cout << " " << mondai[i][j] << " "; //２次元配列を２次元に並べる
}
else {
cout << " " << " " << " "; //２次元配列を２次元に並べる
}
if (j % 3 == 2)cout << "｜";//２本目３本目の縦線
}
if (i % 3 == 2) {
cout << endl;
for (int j = 0; j < 26; j++)cout << " -"; //２本目３本目の横線
}
cout << endl;
}
}
void cellslstkaiseki() {//全体構造解析 = 全セルリスト構造解析
for (int a = 0; a < n; a++) {
for (int b = 0; b < n; b++) {
if (mondai[a][b] == 0) {//解析対象を空欄のみとする
for (int i = 0; i < n; i++)lst[a][b][i] = i + 1;//初期化 1から9までをリスト
for (int i = 0; i < n; i++) {//行の条件によって候補数字を外す
for (int j = 0; j < n; j++) {
if (j != b) {//自己以外のセルによってセルは条件づけられている
if (lst[a][b][i] == mondai[a][j]) {//過去に外されたものはlst[a][b][i]が0になっており、
//等式が成り立たないから問題はない
lst[a][b][i] = 0;//mondai[a][j]を候補数字から外す
}
}
}
}
for (int i = 0; i < n; i++) {//列の条件によって候補数字を外す
for (int j = 0; j < n; j++) {
if (j != a) {//自己以外のセルによってセルは条件づけられている
if (lst[a][b][i] == mondai[j][b]) {//過去に外されたものはlst[a][b][i]が0になっており、
//等式が成り立たないから問題はない
lst[a][b][i] = 0;//mondai[j][b]を候補数字から外す
}
}
}
}
//yとxはそれぞれブロックのトップ＝一番上で一番左のセルの縦座標と横座標
int y = 3 * (a / 3);//aはmondai[a][b]のa
int x = 3 * (b / 3);//bはmondai[a][b]のb
//現在リスト構造解析を受けているセルは(a,b)でありブロック先頭の座標は(y,x)である
//ブロック先頭は(0,0),(0,3),(0,6),(3,0),(3,3),(3,6),(6,0),(6,3),(6,6)と動いている。
//それぞれのブロック先頭の座標をmonddai[a][b]の(a,b)から作り出さなければならない。
for (int i = 0; i < n; i++) {//ブロックの条件によって候補数字を外す
for (int j = 0; j < n; j++) {
if (y + (j / 3) != a || x + (j % 3) != b) {
//自己以外のセルによってセルは条件づけられているから
//自己自身は対象から外す
//自分の本質は、自分の中にはなくて外のセルとの関係によってきまる
if (lst[a][b][i] == mondai[y + (j / 3)][x + (j % 3)]) {
//過去に外されたものはlst[a][b][i]が0になっており、
//等式が成り立たないから問題はない
lst[a][b][i] = 0;//mondai[y + (j / 3)][x + (j % 3)]を候補数字から外す
}
}
}
}
mx[a][b] = 0;//候補数字いったん0に初期化しておく
for (int i = 0; i < n; i++) {
if (lst[a][b][i] > 0) {
lst[a][b][mx[a][b]] = lst[a][b][i];//0となっているところを詰める
mx[a][b]++;
}
}
}
}
}
}
void nextcell(int g) {//次に入力するセルの座標を探索する関数
int mn = 10;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (mondai[i][j] == 0) {//空欄のみをランキング対象にする
if (mx[i][j] < mn) {//<=でないことによって左及び上が優先される
mn = mx[i][j];
Y[g] = i;
X[g] = j;
}
}
}
}
}
void sudokukaiho(int g) {//数独を解くエンジン
nextcell(g);//座標(Y[g], X[g])の取得
for (int i = 0; i < mx[Y[g]][X[g]]; i++) {
mondai[Y[g]][X[g]] = lst[Y[g]][X[g]][i];
//候補の数字を代入 例えば、mondai[0][1]なら{2, 4}の2，4の順に代入する
int y = 3 * (Y[g] / 3);//ブロックの先端（一番上で一番左のセル）のｙ座標
int x = 3 * (X[g] / 3);//ブロックの先端（一番上で一番左のセル）のｘ座標
int gy[9], r[9], b[9];
//gy[j]のjはリスト解析に変更があったセルのｘ座標
//r[j]のjはリスト解析に変更があったセルのｙ座標
//b[j]のjはリスト解析に変更があったセルの座標を(y + (j / 3),x + (j % 3))の形で示す
for (int j = 0; j < n; j++) {
gy[j] = -1;//-1に初期化
r[j] = -1;//-1に初期化
b[j] = -1;//-1に初期化
}
//以降([Y[g]], [X[g]])が所属するY[g]行にあるすべての空欄についてリスト構造解析を行う
for (int j = 0; j < n; j++) {
if (j != X[g]) {//自分自身は解析の対象にしない
if (mondai[Y[g]][j] == 0) {//空欄のみを解析の対象とする
for (int k = 0; k < mx[Y[g]][j]; k++) {
if (mondai[Y[g]][X[g]] == lst[Y[g]][j][k]) {
gy[j] = 1;//jはリスト解析に変更があったセルのｘ座標
mx[Y[g]][j]--;
for (int l = k; l < mx[Y[g]][j]; l++) {
lst[Y[g]][j][l] = lst[Y[g]][j][l + 1];
}
//lst[Y[g]][j][k]はlst[Y[g]][j][k + 1]に置き換わるが
//mondai[Y[g]][X[g]]の値がそのままなので復元可能
break;
}
}
}
}
}
//以上([Y[g]], [X[g]])が所属するY[g]行にあるすべての空欄についてリスト構造解析を行った
//以降([Y[g]], [X[g]])が所属するX[g]列にあるすべての空欄についてリスト構造解析を行う
for (int j = 0; j < n; j++) {
if (j != Y[g]) {//自分自身は解析の対象にしない
if (mondai[j][X[g]] == 0) {//空欄のみを解析の対象とする
for (int k = 0; k < mx[j][X[g]]; k++) {
if (mondai[Y[g]][X[g]] == lst[j][X[g]][k]) {
r[j] = 1;//jはリスト解析に変更があったセルのｙ座標
mx[j][X[g]]--;
for (int l = k; l < mx[j][X[g]]; l++) {
lst[j][X[g]][l] = lst[j][X[g]][l + 1];
//lst[j][X[g][k]はlst[j][X[g][k + 1]に置き換わるが
//mondai[Y[g]][X[g]]の値がそのままなので復元可能
}
}
}
}
}
}
//以上([Y[g]], [X[g]])が所属するX[g]列にあるすべての空欄についてリスト構造解析を行った
//以上[Y[g]][X[g]]が所属するX[g]列にあるすべての空欄についてリスト構造解析を行った
//以降([Y[g]], [X[g]])が所属するブロックにあるすべての空欄についてリスト構造解析を行う
for (int j = 0; j < n; j++) {
if (y + (j / 3) != Y[g] && x + (j % 3) != X[g]) {//行・列で行った解析部分は重複を防ぐために対象外とする
if (mondai[y + (j / 3)][x + (j % 3)] == 0) {//空欄のみを解析の対象とする
for (int k = 0; k < mx[y + (j / 3)][x + (j % 3)]; k++) {
if (mondai[Y[g]][X[g]] == lst[y + (j / 3)][x + (j % 3)][k]) {
b[j] = 1;//のjはリスト解析に変更があったセルの座標を(y + (j / 3),x + (j % 3))の形で示す
mx[y + (j / 3)][x + (j % 3)]--;
for (int l = k; l < mx[y + (j / 3)][x + (j % 3)]; l++) {
lst[y + (j / 3)][x + (j % 3)][l] = lst[y + (j / 3)][x + (j % 3)][l + 1];
//lst[j][X[g]][k]はlst[j][X[g]][k + 1]に置き換わるが
//mondai[Y[g]][X[g]]の値がそのままなので復元可能
}
break;
}
}
}
}
}
//以上([Y[g]], [X[g]])が所属するブロックにあるすべての空欄についてリスト構造解析を行った
//以上[Y[g]][X[g]]が所属するY[g]行にあるすべての空欄についてリスト構造解析を行った
if(g + 1 < tm)sudokukaiho(g + 1);
if (cn1 == 1)return;
if (g == tm - 1) {
hy();
cn1 = 1;
return;
}
//以降復元作業 = 逆部分解析
//以降行部分の復元をおこなう
int q = mondai[Y[g]][X[g]];
mondai[Y[g]][X[g]] = 0;
for (int j = 0; j < n; j++) {
if (gy[j] == 1) {
lst[Y[g]][j][mx[Y[g]][j]] = q;
//順番は書き換わるがメンバーを復元できればよいので問題はない
mx[Y[g]][j]++;
}
}
//以上行部分の復元を行った
//以降列部分の復元を行う
for (int j = 0; j < n; j++) {
if (r[j] == 1) {
lst[j][X[g]][mx[j][X[g]]] = q;
//順番は書き換わるがメンバーを復元できればよいので問題はない
mx[j][X[g]]++;
}
}
//以上列部分の復元を行った
//以降列部分のブロックのを復元をおこなう
for (int j = 0; j < n; j++) {
if (b[j] == 1) {
lst[y + (j / 3)][x + (j % 3)][mx[y + (j / 3)][x + (j % 3)]] = q;
//順番は書き換わるがメンバーを復元できればよいので問題はない
mx[y + (j / 3)][x + (j % 3)]++;
}
}
//以上列部分の復元を行った
}
}
void f(int s) {//ヒント数0の数独を解く関数
int y = s / 9; //縦座標
int x = s % 9; //横座標
unsigned u = (unsigned)time(NULL);
srand(2); //シード整数値を現在の時刻から取得 後に2はuに戻す
int ii = rand() % 9; //始まりをランダムにする
for (int i = 0; i < n; i++) {
sudoku[y][x] = (i + ii) % n + 1; //２次元配列に１から９までの整数を入力
//現時点ではなぜかうまくいっていないが後に原因を解明予定
//例えば、ii = 5でi = 0ならば(5 + 0) % 9 + 1の計算から5になるはずなのに現実は1になっている
//この問題は後に改善する
if (x > 0) {
for (int j = 0; j < x; j++) {
if (sudoku[y][x] == sudoku[y][j])goto tobi; //行の重複を防ぐ
}
}
if (y > 0) {
for (int j = 0; j < y; j++) {
if (sudoku[j][x] == sudoku[y][x])goto tobi; //行の重複を防ぐ
}
}
if (y % 3 == 1) {
for (int j = 0; j < 3; j++) {
if ((x / 3) * 3 + j != x) {
if (sudoku[y][x] == sudoku[y - 1][(x / 3) * 3 + j])goto tobi; //ブロックの重複を防ぐ
}
}
}
if (y % 3 == 2) {
for (int j = 0; j < 3; j++) {
if ((x / 3) * 3 + j != x) {
if (sudoku[y][x] == sudoku[y - 2][(x / 3) * 3 + j])goto tobi; //ブロックの重複を防ぐ
if (sudoku[y][x] == sudoku[y - 1][(x / 3) * 3 + j])goto tobi; //ブロックの重複を防ぐ
}
}
}
if (s + 1 < n * n)f(s + 1); //１つ奥の部屋に入室
if (cn == 1)return; //数独が1個できた時点で止める
if (sng == 0)return; //異常があった時点でプロジェクトを止める
if (s == n * n - 1) { //一番奥の部屋に到達
int hb; //部屋番号
int tbs[6] = { 11,13,17,19,23,29 }; //飛びの選択肢 素数であれば81と互いに素は保証されている
int st = rand() % 81; //始めの位置
int tb = tbs[rand() % 6]; //飛び
int h = 0; //可否の否
int* gohr = (int*)calloc(hnt, sizeof(int));
for (int t = 0; t < hnt; t++) {
gohr[t] = (st + t * tb) % 81;
}
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
hb = n * j + k; //部屋番号の再初期化 = 空欄の数字候補の個数の小さい順に入れる
int h = 0; //可否の否
for (int t = 0; t < hnt; t++) {
if (gohr[t] == hb) {
h = 1;//可否の可
break;
}
}
if (h == 1) {
mondai[j][k] = sudoku[j][k]; //問題用の配列に代入
}
}
}
hy();
free(gohr); //メモリ解放
int p[9];//重複検査のための配列
int kr;
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++)p[k] = 0;//初期化
kr = 1; //初期化
for (int k = 0; k < n; k++) {
p[sudoku[j][k] - 1] = 1;
}
for (int k = 0; k < n; k++) {
if (p[k] == 0) { //行の重複検査
cout << "×";
kr = 0;
sng = 0;
goto tobi1;
}
}
for (int k = 0; k < n; k++)p[k] = 0;//初期化
kr = 1; //初期化
for (int k = 0; k < n; k++) {
p[sudoku[k][j] - 1] = 1;
}
for (int k = 0; k < n; k++) {
if (p[k] == 0) { //列の重複検査
cout << "×";
kr = 0;
sng = 0;
goto tobi1;
}
}
for (int k = 0; k < n; k++)p[k] = 0;//初期化
kr = 1; //初期化
for (int k = 0; k < n; k++) {
p[sudoku[3 * (j / 3) + (k / 3)][3 * (j % 3) + (k % 3)] - 1] = 1;
}
for (int k = 0; k < n; k++) {
if (p[k] == 0) {//ブロックの重複検査
cout << "×";
kr = 0;
sng = 0;
goto tobi1;
}
}
}
tobi1:;
if (kr == 1)cout << "〇";
cn++;
if (cn == 1)return; //数独が1個できた時点でとめる
}
tobi:;
}
}
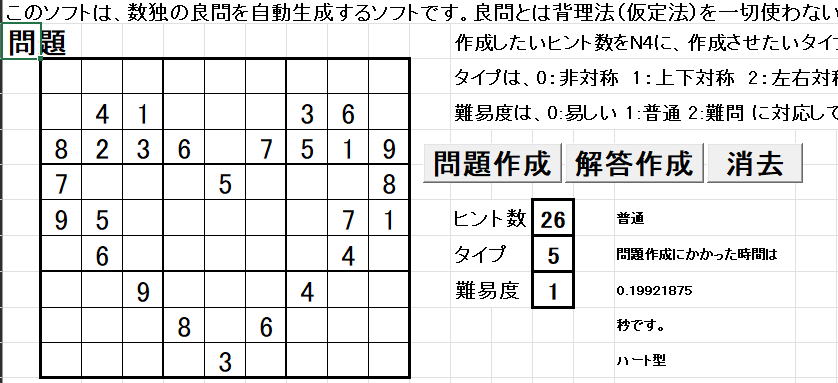
というページが開きます。
タスクバーにあるこれをクリック）を起動して、
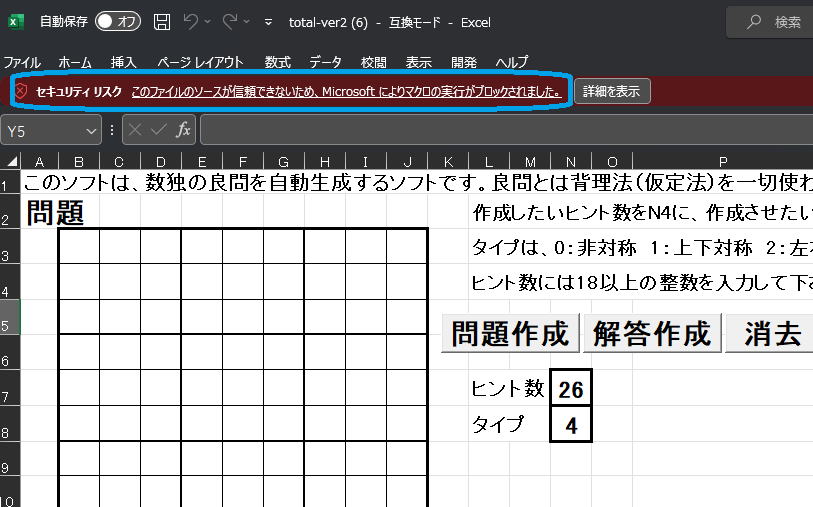マイクロソフトによってブロックされ、マクロが使えない状態になります。ですので、右上の
の×をクリックしてエクセルを閉じてください。エクスプローラー（
それで、total-ver2（私の場合何回もクリックしたために(8)という余計なものが付いていますが）を右クリックします。そして、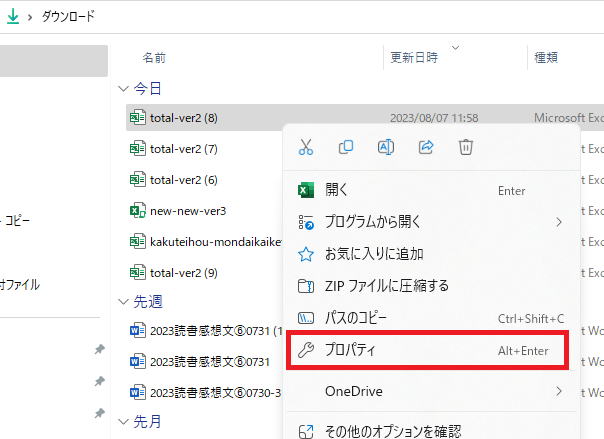
プロパティをクリックします。
下の方にある許可をするにチェクマークを入れて入れてOKボタンを押します。そして、total-ver2をダブルクリックしてください。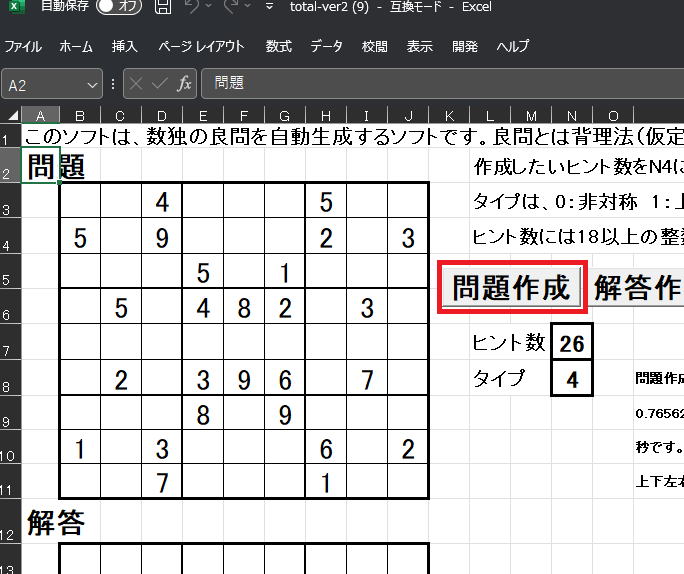
ヒント数とタイプに適当な数字を入力して、