第4話 疑似数独の実現

・
・
・

を実現するプログラム例
#include<iostream>
#include<conio.h> //while (!_kbhit()); を使うためのお呪い。
using namespace std;
void f(int s); //sは次元番号=部屋番号
int n; //次元数(部屋数)をキーボードから指定
int cn = 0; //順列を数える変数
int m[9][9];//本体2次元配列(魔方陣の研究から始まったので本体をmとしてきた
int main() {
//cout << "n = ";
//scanf_s("%d", &n); //キーボードからnの値を取得
n = 9;
clock_t hj, ow;
hj = clock();
f(0);
ow = clock();
cout << "計算時間は" << (double)(ow - hj) / CLOCKS_PER_SEC << "秒です。" << endl;
cout << "順列の場合の数は" << cn << "です。" << endl;
cout << "プロジェクト成功" << endl;
while (!_kbhit()); //待機させるための命令
return(0);
}
void f(int s) {
int y = s / 9; //縦座標
int x = s % 9; //横座標
for (int i = 0; i < n; i++) {
m[y][x] = i + 1; //2次元配列に1から9までの整数を入力
if (x > 0) {
for (int j = 0; j < x; j++) {
if (m[y][x] == m[y][j])goto tobi; //行の重複を防ぐ
}
}
if (y > 0) {
for (int j = 0; j < y; j++) {
if (m[j][x] == m[y][x])goto tobi; //行の重複を防ぐ
}
}
if (s + 1 < n * n)f(s + 1); //1つ奥の部屋に入室
if (cn == 100)return; //模擬数独が100個で来た時点でとめる
if (s == n * n - 1) { //一番奥に部屋に到達
cout << endl;
for (int j = 0; j < 17; j++)cout << " -"; //最初の横線
cout << endl;
for (int j = 0; j < n; j++) {
cout << "|"; //縦線
for (int k = 0; k < n; k++) {
cout << " " << m[j][k] << " "; //2次元配列を2次元に並べる
if (k % 3 == 2)cout << "|";//縦線
}
if (j % 3 == 2) {
cout << endl;
for (int k = 0; k < 17; k++)cout << " -"; //横線
}
cout << endl;
}
cn++;
if (cn == 100)return; //模擬数独が100個で来た時点でとめる
}
tobi:;
}
}
では最後の条件ブロックを加えてヒント数0の自動生成に挑戦しましょう。
ブロックの条件は難しいですのでヒントを書いておきます。
*エクセルではマスのことをセルと言います。
部屋番号は魔方陣のときのように条件が厳しい直線(魔方陣の場合は対角線)は存在しませんので、
とします。
(注)各部屋は任務が終了した時点で消滅します。
例えば、元セルが50(s = 50)の位置にいるならば、
51以降の部屋は存在していません。
関数の再帰的使用の場合は、各部屋は生成消滅をくりかえしていることを忘れないでください。
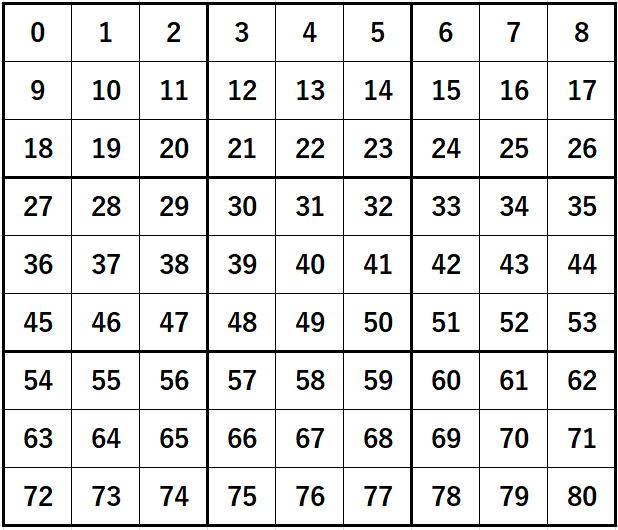
ブロックの重複検査が必要なセルは
色の塗ってあるところです。
m[j][k]が白のセルにあるときは、行重複検査・列重複検査により、
重複検査が済んでいるからです。
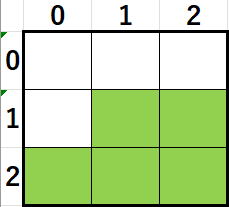
では、対称セル(現在いるセル図のときに)は、
検査するセルはどれでしょうか。
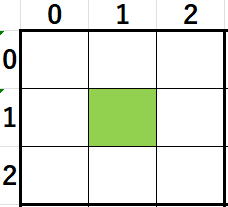
答えは
オレンジのセルです。
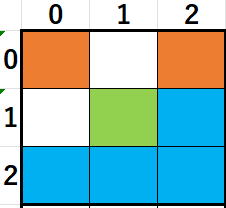
青のセルはまだ存在していませんから比較の必要がありません。
(0,1)の白のセルは列重複チェックでだぶり検査は済んでいます。
(1,0)の白のセルは行重複チェックで重複検査な済んでいます。
では、問題です。
現セルが
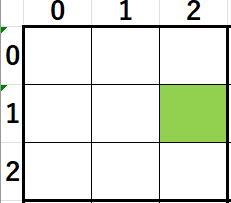
にいる場合の重複検査が必要なのはどのセルでしょうか。
答えは20行下に書きます。
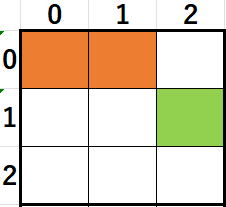
オレンジです。
行2は未来ですからまだ存在していませんから考える必要はありません。
行1の白いセルは行重複検査が済んでいます。
行0の白いセルは列重複検査が済んでいます。
一言でまとめると、
(解答は20行下)
検査対象となるセルは過去セルで現セルと同一直線上にないセルです。
要するに同じ行または同じ列については検査が済んでいますので、
検査が必要ないわけです。
さあ、数独自動生成(=ヒント数0の数独を解く)を実現してください。

・
・
・

第3話へ 第5話へ
トップ