第6章 6次魔方陣・8次魔方陣の作成
第5話 for文を使って対角線部分の交換をすっきりさせる!
⁂私が2022を使っている間に2026の設定が変わってしまっています。
 がUTF‑8になっている場合にはShift-JISに変更して
がUTF‑8になっている場合にはShift-JISに変更して エンコード付きで保存してください。⁂
エンコード付きで保存してください。⁂マルチスレッド版数独自動生成ソフトC++コードを題材とする超初心者のためのVisual Studio C++講義
第6章 6次魔方陣・8次魔方陣の作成
第5話 for文を使って対角線部分の交換をすっきりさせる!
⁂私が2022を使っている間に2026の設定が変わってしまっています。
 がUTF‑8になっている場合にはShift-JISに変更して
がUTF‑8になっている場合にはShift-JISに変更して
 エンコード付きで保存してください。⁂
エンコード付きで保存してください。⁂
対角線部分を交換して
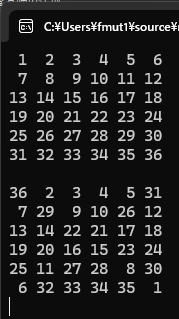
(
1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30
31 32 33 34 35 36
36 2 3 4 5 31
7 29 9 10 26 12
13 14 22 21 17 18
19 20 16 15 23 24
25 11 27 28 8 30
6 32 33 34 35 1
)
を実現するコード例
#include<iostream>//インクルードファイルiostreamの読み込み
#include<conio.h>//while(!_kbhit());を使うためのお呪い
#include<string> //文字列変数を使えるようにするために組み込む
#include <iomanip> //setprecisionを使えるように組み込む
#include <cmath>//powなどを使うときに必要
#include <ctime>//time()(←現時刻発生する関数)を使うために必要
using namespace std;//coutを使うときに必要なお呪い
void 魔方陣();//横と縦の2方向を持つ2次元for文体験
const int n = 6;//これからは具体的な数字を使わずにnとする。左の6を8などに変更すれば8次魔方陣に対応する
//n = 6 の一か所だけ具体的な数字を使い、他ではすべて n を使ってください。
int main() {//私は社長だ。
魔方陣();
while (!_kbhit());//待機させるための命令
return(0);//int main()終わるためのお呪い
}
void 魔方陣() {
int a[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = n * i + j + 1;//自然配列を生成してaに収納する
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//自然配列に体裁を整えて表示する。
if (a[i][j] < 10)cout << " ";
cout << a[i][j]<<" ";
}
cout << endl;
}
cout << endl;
int 受け皿;//a[i][j]などのデータを一時保存する
//対角線部分を交換する
for (int i = 0; i < 3; i++) {
受け皿 = a[i][i];
//a[i][i]のデータがa[n - 1 - i][n - 1 - i]のデータに上書きされる前に受け皿に保存
a[i][i] = a[n - 1 - i][n - 1 - i];
//a[i][i]のデータをa[n - 1 - i][n - 1 - i]のデータで上書き
a[n - 1 - i][n - 1 - i] = 受け皿;
//a[n - 1 - i][n - 1 - i]のデータをa[i][i]の元データで保存
}
//対角線部分の交換終了
//逆対角線部分を交換する
for (int i = 0; i < 3; i++) {
受け皿 = a[i][n - 1 - i];
//a[i][n - 1 - i]のデータがa[n - 1 - i][i]のデータに上書きされる前に受け皿に保存
a[i][n - 1 - i] = a[n - 1 - i][i];
//a[i][n - 1 - i]のデータをa[n - 1 - i][i]のデータで上書き
a[n - 1 - i][i] = 受け皿;
//a[n - 1 - i][i]のデータをa[i][n - 1 - i]の元データで保存
}
//逆対角線部分の交換終了
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//対角線分を交換した配列に体裁を整えて表示する。
if (a[i][j] < 10)cout << " ";
cout << a[i][j] << " ";
}
cout << endl;
}
}
課題を出した本人(つまり、私)も
//対角線部分を交換する
for (int i = 0; i < 3; i++) {
受け皿 = a[i][i];
//a[i][i]のデータがa[n - 1 - i][n - 1 - i]のデータに上書きされる前に受け皿に保存
a[i][i] = a[n - 1 - i][n - 1 - i];
//a[i][i]のデータをa[n - 1 - i][n - 1 - i]のデータで上書き
a[n - 1 - i][n - 1 - i] = 受け皿;
//a[n - 1 - i][n - 1 - i]のデータをa[i][i]の元データで保存
}
//対角線部分の交換終了
//逆対角線部分を交換する
for (int i = 0; i < 3; i++) {
受け皿 = a[i][n - 1 - i];
//a[i][n - 1 - i]のデータがa[n - 1 - i][i]のデータに上書きされる前に受け皿に保存
a[i][n - 1 - i] = a[n - 1 - i][i];
//a[i][n - 1 - i]のデータをa[n - 1 - i][i]のデータで上書き
a[n - 1 - i][i] = 受け皿;
//a[n - 1 - i][i]のデータをa[i][n - 1 - i]の元データで保存
}
//逆対角線部分の交換終了
にはびっくり仰天です。
こんなにすっきりするとは!
for文は偉大なり!
| 36 | 2 | 3 | 4 | 5 | 31 |
| 7 | 29 | 9 | 10 | 26 | 12 |
| 13 | 14 | 22 | 21 | 17 | 18 |
| 19 | 20 | 16 | 15 | 23 | 24 |
| 25 | 11 | 27 | 28 | 8 | 30 |
| 6 | 32 | 33 | 34 | 35 | 1 |
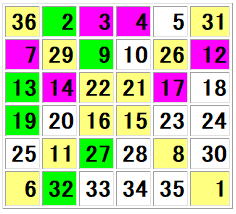 (同じものを図にしました)
(同じものを図にしました)
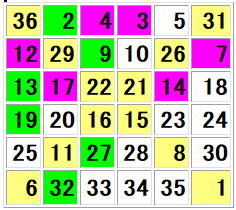
さて、次に課題は明るい紫部分を中央の直線に対して左右に線対称移動をさせることです。
| 36 | 2 | 4 | 3 | 5 | 31 |
| 12 | 29 | 9 | 10 | 26 | 7 |
| 13 | 17 | 22 | 21 | 14 | 18 |
| 19 | 20 | 16 | 15 | 23 | 24 |
| 25 | 11 | 27 | 28 | 8 | 30 |
| 6 | 32 | 33 | 34 | 35 | 1 |
 (同じものを図にしました)
(同じものを図にしました)
これもfor文で実現してください。
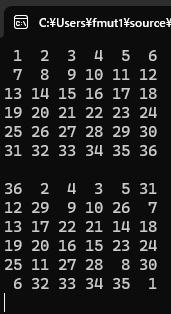
(
1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30
31 32 33 34 35 36
36 2 4 3 5 31
12 29 9 10 26 7
13 17 22 21 14 18
19 20 16 15 23 24
25 11 27 28 8 30
6 32 33 34 35 1
)
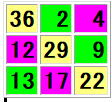
ヒントは
| 36 | 2 | 4 |
| 12 | 29 | 9 |
| 13 | 17 | 22 |
 (同じものを図にしました)
(同じものを図にしました)
の明るい紫の座標をどのように制御変数 i を使ってどう制御するかです。
相手方は線対称なのでそれがわかれば自動的に決まります。
さらなるヒントとして座標C++形式で書いておきます。
a[0][2]
a[1][0]
a[2][1]
つまり、 2,0,1 を 0,1,2 でどう表すかです。
第3のヒントして % をうまく利用するです。
第6章第4話へ 第6章第6話へ
本講義トップへ