第5章 配列
第9話 第4章第14話のコードを2次元for文で書き換える
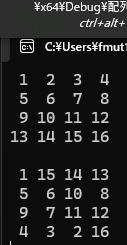
第4章第14話課題を2次元配列での改良
(
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
1 15 14 13
5 6 10 8
9 7 11 12
4 3 2 16
)
2次元配列で実現するコード例
#include<iostream>//インクルードファイルiostreamの読み込み
#include<conio.h>//while(!_kbhit());を使うためのお呪い
#include<string> //文字列変数を使えるようにするために組み込む
#include <iomanip> //setprecisionを使えるように組み込む
#include <cmath>//powなどを使うときに必要
#include <ctime>//time()(←現時刻発生する関数)を使うために必要
using namespace std;//coutを使うときに必要なお呪い
void 2次元for文();//横と縦の2方向を持つ2次元for文体験
int main() {//私は社長だ。
2次元for文();
while (!_kbhit());//待機させるための命令
return(0);//int main()終わるためのお呪い
}
void 2次元for文() {
//横と縦の2方向を持つ2次元for文体験
int a[4][4];//4行4列の行列を表すことのできる2次元配列の宣言
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
a[i][j] = 4 * i + j + 1;
}
}
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if (a[i][j] < 10)cout << " ";
cout << a[i][j] << " ";
}
cout << endl;
}
//以下
//a[0][1]とa[3][2]の交換
//a[0][2]とa[3][1]の交換
//a[1][0]とa[2][3]の交換
//a[2][0]とa[1][3]の交換
int 受け皿;//a[0][1]などのデータを一時的に預かる変数
//a[0][1]とa[3][2]の交換
受け皿 = a[0][1];//a[0][1]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[0][1] = a[3][2];
//a[0][1]のデータがa[3][2]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[3][2] = 受け皿;
//a[0][1]の元のデータをa[3][2]に入力
//a[0][1]とa[3][2]の交換終了
//a[0][2]とa[3][1]の交換
受け皿 = a[0][2];//a[0][2]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[0][2] = a[3][1];
//a[0][2]のデータがa[3][1]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[3][1] = 受け皿;
//a[0][2]の元のデータをa[3][1]に入力
//a[0][2]とa[3][1]の交換終了
//a[1][0]とa[2][3]の交換
受け皿 = a[1][0];//a[0][1]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[1][0] = a[2][3];
//a[1][0]のデータがa[2][3]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[2][3] = 受け皿;
//a[1][0]の元のデータをa[3][2]に入力
//a[0][1]とa[2][3]の交換終了
//a[2][0]とa[1][3]の交換
受け皿 = a[2][0];//a[2][0]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[2][0] = a[1][3];
//a[2][0]のデータがa[1][3]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[1][3] = 受け皿;
//a[2][0]の元のデータをa[1][3]に入力
//a[2][0]とa[1][3]の交換終了
cout << endl;
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if (a[i][j] < 10)cout << " ";
cout << a[i][j] << " ";
}
cout << endl;
}
}
このあと3次魔方陣の自動生成と4×4数独自動生成に取り組む予定でしたが、
これは次元数でいうとそれぞれ9次元と16次元に対応します。
もちろん、9次元for文や16次元for文をやると頭が混乱するので、
それはやめて次の章で関数の再帰的使用という方法を学び、
再帰的方法によって3次魔方陣・4次魔方陣・5次魔方陣の自動生成、
4×4数独自動生成に取り組みます。
そして、この章の第10話と第11話と第12話は4次魔方陣の

(
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
1 15 14 13
5 6 10 8
9 7 11 12
4 3 2 16
)
の検証という作業に取り組みます。
検証内容は
①
4つの行・4つの列・2つの対角線の合計が
(1 + 2 + ・・・ +16)÷4 = 34
になっているか調べる
②
1~16までの数字が1つずつあるのかを調べます。
②については1~16の自然配列の一部の整数を点対称移動によって交換しただけですから、
本来不要な作業です。
ですが、奇数次魔方陣を生成するときに整数を商と余りに分解して、
商と余りの4つの行・4つの列・2つの対角線の合計が同じなるようにしてから、
合体するという方法をとります。
このとき商と余りが同じ時に合体時にできる整数が重複してしますので、
重複検査が不可欠となります。
ですが、②は作ってみると大変困難な作業であり、
この章で扱うのは無理と判断しました。
②は第6章か第7章にいどうします。
ですから、検証は①のみとなります。
まず、配列
int 行合計[4] = { 0,0,0,0 };
//各行の合計を出す配列を定義して、すべてを0に初期化
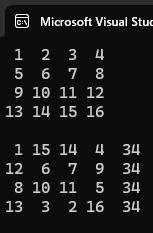
を定義して、行合計を計算して
(
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
1 15 14 4 34
12 6 7 9 34
8 10 11 5 34
13 3 2 16 34
)
となるようにコードを改良してください。
第5章第8話へ 第5章第10話へ
本講義トップへ