第3章 for文(繰り返し処理)
第1話 for文を体験するための準備
いよいよ繰り返し処理のfor文に入ります。
前にも申し上げましたが、
for文を学べば 1 + 2 + ・・・ + 10 どころでなく
1 + 2 + ・・・ + 100 も 1 + 2 + ・・・ + 10000 もあっという間に計算できてしまいます。
この章で学ぶfor文と次の章で学ぶif文を学べば、
プログラミングの世界は一気に広がります。
私の記憶によると、
繰り返し処理とif文を使えれば、
あらゆるプログラムが組めることが数学的に証明されています。
さて、すぐに取り組みたいところですが、
コードが大きくなりすぎましたので、
新しいプロジェクトを作成して、
最初からやり直したいと思います。
まず、Visual Studio 2026を起動してください。

そして画面一番右側の
新しいプロジェクトの作成(N)をクリックします。
そして、赤い矢印の通り下にスクロールします。
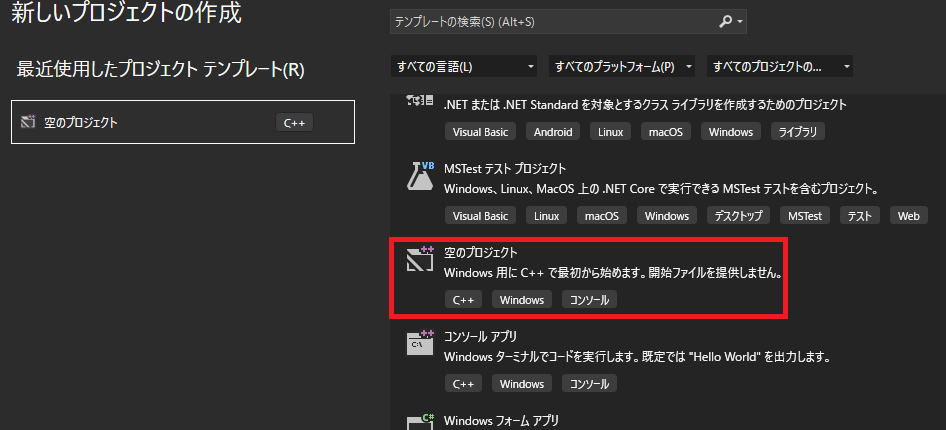
空のプロジェクトを選び、
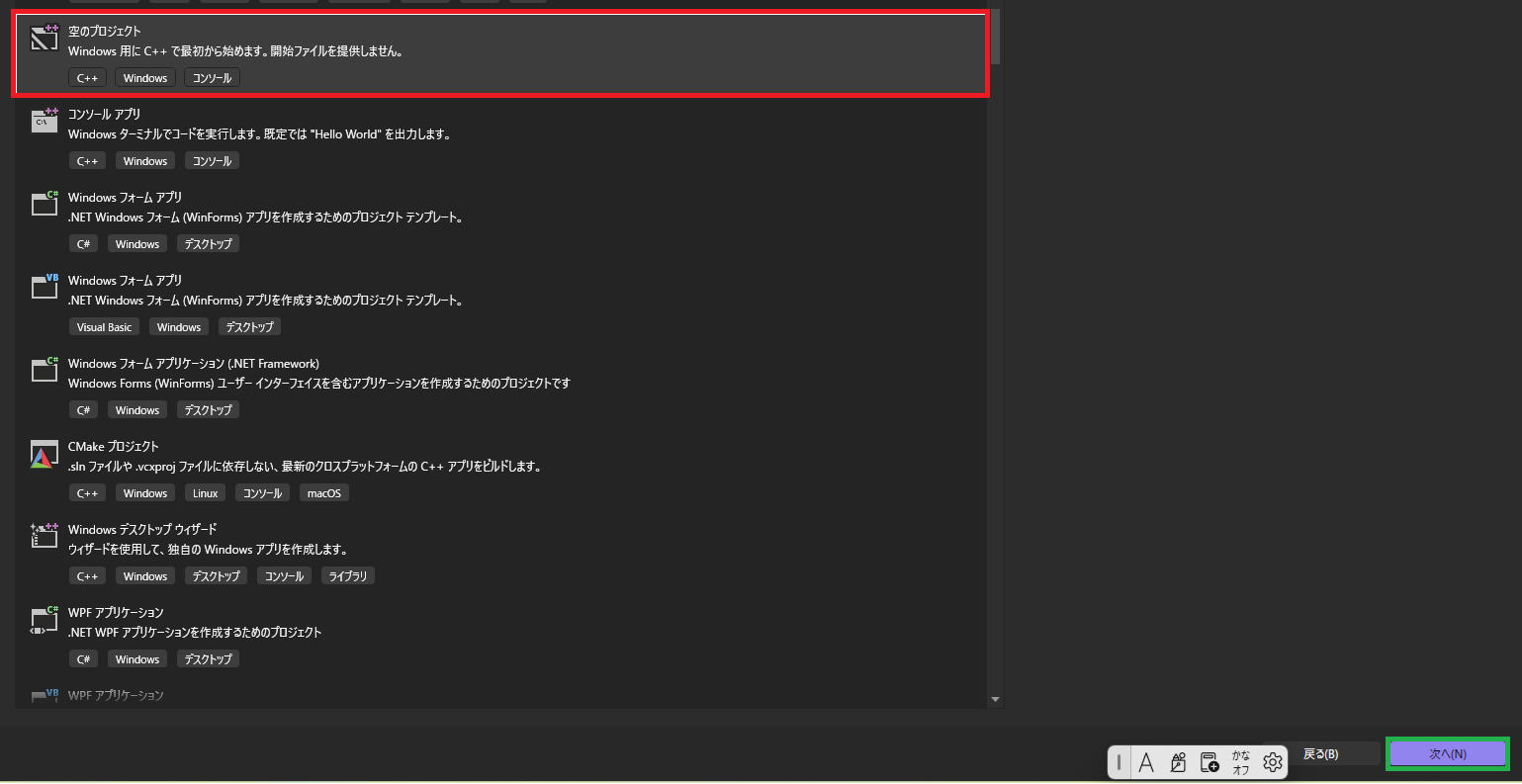
次へ(N)をクリックします。
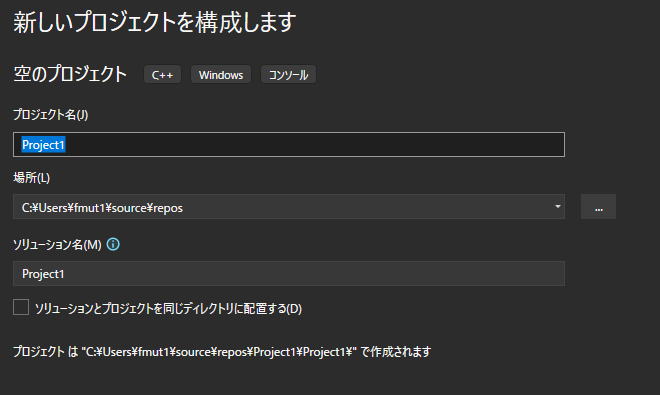
プロジェクト名をfor文体験(もちろん名前ですから禁則さえ侵さなければ何でもよいです)としましょう。
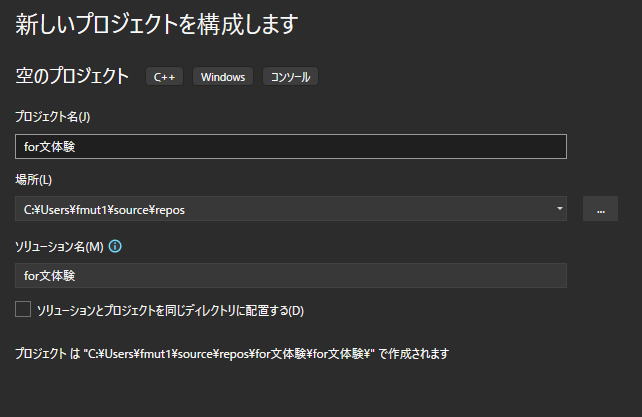
そして、一番右下の
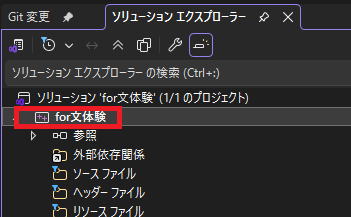
ソリューションエクスプローラーのfor文体験のところで右クリック
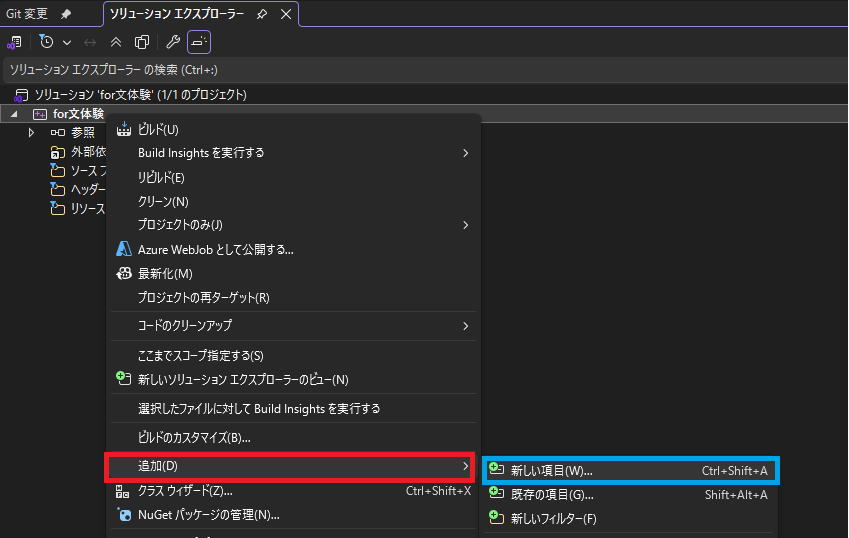
(私の場合はソリューションエクスプローラーが一番左にあるので右側展開となっていますが、
一番右にある場合は左側展開となります)
→追加→新しい項目の順に選び
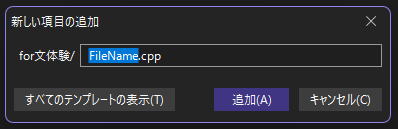
はこのまま追加してください。
もちろん、プログラミングの体験がある方は別の名前でも結構ですが、
私の説明画面と違ってしまいますので、
できれば名前を変更せずに追加してください。すると
エディタ(プログラミング専用編集ソフト)が出てきます。
そして、以下のコードをコピペしてください。
#include<iostream>//インクルードファイルiostreamの読み込み
#include<conio.h>//while(!_kbhit());を使うためのお呪い
using namespace std;//coutを使うときに必要なお呪い
#include<conio.h>//while(!_kbhit());を使うためのお呪い
#include<string> //文字列変数を使えるようにするために組み込む
#include <iomanip> //setprecisionを使えるように組み込む
int 足し算();//1 + 2 + ・・・ + 100 などを計算する関数
int main() {//私は社長だ。
cout << "さぁ、探検・冒険の始まりだ!" << endl;
while (!_kbhit());//待機させるための命令
return(0);//int main()終わるためのお呪い
}
int 足し算() {
//1 + 2 + ・・・ + 100 などを計算する関数
return(0);//何かを返さないとエラーしますのでとりあえず0を返していますが、後に変更されます。
}
⁂このタイミングで以下が必要となります。
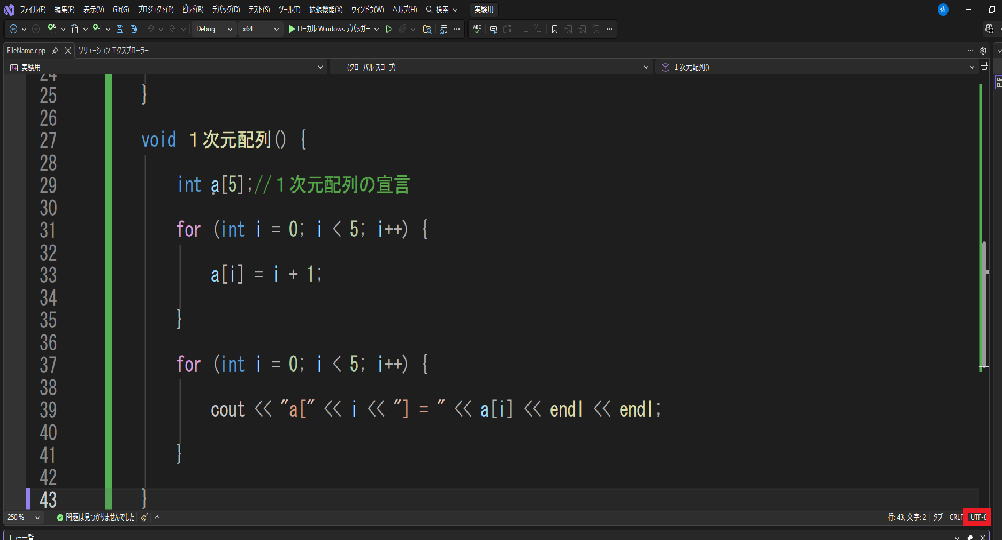
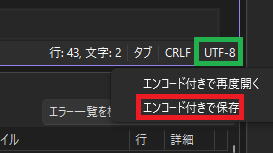
緑の囲いがUTF-8になっている場合は、
以下を必ず実行してください。
UTF-8をクリック→エンコード付きで保存
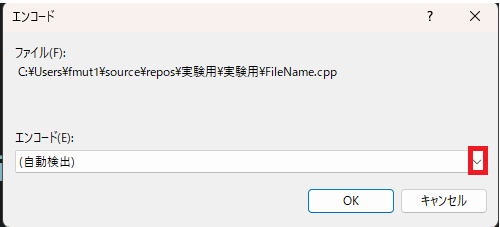
赤い囲いをクリック
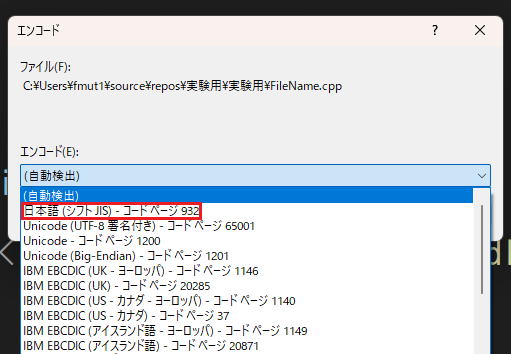
日本語(シフトJIS)-コードページ932を選択
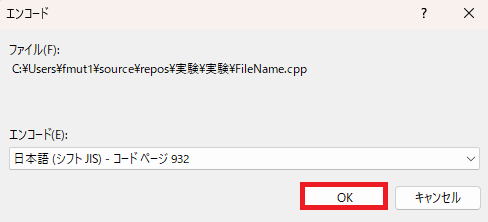
OKを選択
 SfitJISになれば問題なしです。⁂
SfitJISになれば問題なしです。⁂実行画面
(さぁ、探検・冒険の始まりだ!)
以上で準備完了です。
探検・冒険の始まりなのでしょうか。
本格的には第4章のif文を学ばないと、
魔方陣の自動生成には挑戦できませんが、
for文によってできることが格段に増えるからです。
尚、魔方陣とは

という正方形です。
方陣とは正方形という意味です。
一辺が3のとき3次魔方陣といいます。
特徴は何ですか。
よく観察してください。解答は20行下。
解答 各行の合計値・各列の合計値・各対角線の合計値はすべて同じ15になっています。
2次魔方陣だけは存在せず、
3次以上についてはすべて存在することがわかっています。
奇数次魔方陣については一般的な作成方法が知られていたのに対して、
偶数次魔方陣については一般的方法が知られていませんでしたが、
私が、二つの方法を発見しています。
足し算的手法と法則性を持つマスの左右対称移動・上下対称移動・点対称移動による方法です。
詳しくは小学生・中学生のための魔方陣授業
を参照してください。
どんな小さな発見でも、
人類が成し遂げていない何かを発見することが、
私の夢でしたが、
偶数次魔方陣に関してはそれを成し遂げたようです。
そして、この魔方陣生成は数学の未解決問題であるP対NP問題のNP完全問題であることがわかっており、
NP完全問題(NP問題の中でも難しい問題)の一つでもPにひっくり返すと、
オセロのようにすべてのNP問題がP問題にひっくり返されることが証明されており、
その場合はP=NPが証明されるというとても大切な問題です。
さらに、いうと一般化された数独もNP完全問題であることが証明されていますので、
数独をP問題にひっくり返しても数学の未解決問題が解決され、
P=NPが証明されることになります。
P問題とは1+2+・・・+10のような簡単な問題のことであり、
問題のサイズ(1+2+・・・+10の場合は10ということになります)多項式時間で解ける問題です。
多項式とはサイズをnとすると
一方NP問題は解くのに指数関数時間かかる問題です。
指数関数とは
 というような関数です。
というような関数です。n = 1 →
 = 10
= 10n = 2 →
 = 100
= 100n = 3 →
 = 100
= 100n = 4 →
 = 1000
= 1000n = 5 →
 = 100000
= 100000n = 6 →
 = 1000000
= 1000000 は1の右に0がn個並ぶ整数です。
は1の右に0がn個並ぶ整数です。と急速に大きくなっていってnが1000辺りではパソコンでは歯が立ちません。
nが100000辺りになるとスパコンでも苦戦します。
第2章第15話へ 第3章第2話へ
本講義トップへ