�g��t�F���}�[�_���ڎ�
�]���藝�ɂ����鎩�R������i�g������������j
���_�i���j���[�j
�P�D
�����P�^�Q�̏ꍇ
�Q�D
�����O�̏ꍇ
�R�D
�����|�P�^�Q�̏ꍇ
�S�D
�����P�^�Q�C�����O�C�|�P�������P�̏ꍇ
���g������������
�@�P�D�@![]() �̏ꍇ
�̏ꍇ
�Q�D�@![]() �̏ꍇ
�̏ꍇ
������![]() �͎��R�����������B
�͎��R�����������B
�i�g��t�F���}�[���j
�@�@ �P�@�����Q�̏ꍇ
�@�@![]()
�A�@![]()
�B�@![]() �ɂ����āA
�ɂ����āA![]() �̗������L�����̕������łȂ��̂ɁA����������
�̗������L�����̕������łȂ��̂ɁA����������
�C�@![]() �͉�������݂���Ȃ�A�����ɂ����B
�͉�������݂���Ȃ�A�����ɂ����B
�]���藝�ɂ����鎩�R�����ɂ���

�@�]���藝![]()
![]() �ɂ����āA�������b���������ł���Ȃ�A���R�����i���A���A���j�����݂��Ȃ����Ƃ͎����ł���B�Ȃ��Ȃ�A�i���A���A���j�����R���ł���Ɖ��肷��ƁA
�ɂ����āA�������b���������ł���Ȃ�A���R�����i���A���A���j�����݂��Ȃ����Ƃ͎����ł���B�Ȃ��Ȃ�A�i���A���A���j�����R���ł���Ɖ��肷��ƁA
�@�@�@�@![]()
�̎�����A���ӂ͖������ʼnE�ӂ͗L�����ƂȂ��Ė������Ă��܂�����ł���B
�@�ł͂������b���L�����ŁA�|�P���������b���P�����Ƃ��A���R�����i���A���A���j�͑��݂���ł��낤���B���̘_���ł͂��̖��ɂ��čl���Ă݂����B
�@�Ȃ��A���R���������݂���Ƃ������ƂƁA���̗L�����������݂���Ƃ����͓̂��l�ł���B�Ȃ��Ȃ�A�L�������i���A���A���j�����݂���ꍇ���A���A���̕���̌��{����������Ύ��R�����i���A���A���j�ɂ��邱�Ƃ��ł��邩��ł���B
�@�������A�������b���L�����ł���A���A���A���͕K���L�����ł���Ƃ����킯�ł͂Ȃ��B![]() �Ȃǂ�����ł��������邱�Ƃ��ł��邩��ł���B
�Ȃǂ�����ł��������邱�Ƃ��ł��邩��ł���B
�@�肪����邽�߂ɁA��̓I�Ȑ��l�ōl���Ă݂邱�Ƃɂ��悤�B�b���U�O���A�X�O���A�P�Q�O���̏ꍇ�A���Ȃ킿�������b�����Ƃ�����![]() �̏ꍇ�ɂ��čl���Ă݂悤�B�i�����܂ł��Ȃ����Ƃł��邪�A�b���X�O���̏ꍇ�̓s�^�S���X���ɂȂ�B�j���ɂ�����q���g�Ɉ�ʓI�ȏꍇ���l���Ă݂悤�B
�̏ꍇ�ɂ��čl���Ă݂悤�B�i�����܂ł��Ȃ����Ƃł��邪�A�b���X�O���̏ꍇ�̓s�^�S���X���ɂȂ�B�j���ɂ�����q���g�Ɉ�ʓI�ȏꍇ���l���Ă݂悤�B
1.
�����P�^�Q�̏ꍇ
2.
�����O�̏ꍇ
3.
�����|�P�^�Q�̏ꍇ
4.
�����P�^�Q�C�����O�C�|�P�������P�̏ꍇ
�P�D�b���U�O���̏ꍇ
�@�@�@![]()
�����ŁC
�������|���C�������|���Ƃ����ƁC
![]()
�����W�J���Ă��ɂ��Đ�������ƁC
![]()
�����ŁC![]() �̂Ƃ��C
�̂Ƃ��C
![]()
![]()
![]()
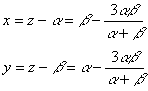
�@�@���ꂼ��̗��ӂɃ��{����������ƁC
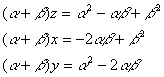
![]()
�i���{���j���C�i���{���j���C�i���{���j�������ꂼ��C���C���C���ƒu�������ƁC
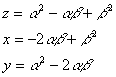
����āC�����O�̂Ƃ��͏\���傫�����ɑ��āC�����O�C�����O�C�����O�ɂȂ�B�܂��C�����O�̂Ƃ��͏\�����������ɑ��āC�����O�C�����O�C�����O�ƂȂ�B
�b���U�O�����炚�͍ő�ӂł͂��蓾�Ȃ��B�����ő�ӂł���Ɖ��肷��ƁC�����O�C�����O�ŁC
![]()
����\�����������ɑ���![]() �����C���C���C���͎O�p���������Ă���B�����ő�ӂł���Ɖ��肷��ƁC�����O�C�����O�ŁC
�����C���C���C���͎O�p���������Ă���B�����ő�ӂł���Ɖ��肷��ƁC�����O�C�����O�ŁC
![]()
![]() �����C���C���C���͎O�p���������Ă���B
�����C���C���C���͎O�p���������Ă���B
�ȏォ��C���R�����͖����ɑ��݂��邱�Ƃ������ꂽ�B
�@�������̉��������Ă݂悤�B
�@
�����P�̂Ƃ�
�@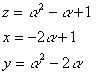
�@�@�����|�P�Ƃ����
�@�@�����R�C�����R�C�����R
�@�@����͐�قǂ̐��O�p�`�i���C���C���j���i�P�C�P�C�P�j�Ɠ������ł���B
�A�@�����|�Q�Ƃ����
�@�@�����V�C�����T�C�����W
�@����āC�i���C���C���j���i�T�C�W�C�V�j
�B�@�����|�R�Ƃ���ƁC
�@�@�����P�R�C�����V�C�����P�T
�@�@����āC�i���C���C���j���i�V�C�P�T�C�P�R�j
�C�@�����|�S�Ƃ���ƁC
�@�@�����Q�P�C�����X�C�����Q�S
�@�@����āC�i���C���C���j���i�R�C�W�C�V�j
�D�@�����|�T�Ƃ���ƁC
�@�@�����R�P�C�����P�P�C�����R�T
�@�@����āC�i���C���C���j���i�P�P�C�R�T�C�R�P�j
�E�@�����|�U�Ƃ���ƁC
�@�@�����S�R�C�����P�R�C�����S�W
�@�@����āC�i���C���C���j���i�P�R�C�S�W�C�S�R�j
�A
�����Q�̂Ƃ�
�@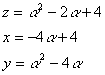
�@�@�����|�P�Ƃ���ƁC
�@�@�����V�C�����W�C�����T
�@�@����āC�i���C���C���j���i�W�C�T�C�V�j
�A�@�����|�Q�Ƃ���ƁC
�@�@�����P�Q�C�����P�Q�C�����P�Q
�@�@����āC�i���C���C���j���i�P�C�P�C�P�j
�B �����|�R�Ƃ���ƁC
�@�@�����P�X�C�����P�U�C�����Q�P
�@�@����āC�i���C���C���j���i�P�U�C�Q�P�C�P�X�j
�C�@�����|�S�Ƃ���ƁC
�@�@�����Q�W�C�����Q�O�C�����R�Q
�@�@����āC�i���C���C���j���i�T�C�W�C�V�j
�D�@�����|�T�Ƃ���ƁC
�@�@�����R�X�C�����Q�S�C�����S�T
�@�@����āC�i���C���C���j���i�W�C�P�T�C�P�R�j
�E�@�����|�U�Ƃ���ƁC
�@�@�����T�Q�C�����Q�W�C�����U�O
�@�@����āC�i���C���C���j���i�V�C�P�T�C�P�R�j
�@
�ƇA�͏d�������邪�C���炩�ɈႤ�����n������o���Ă���B���̒l�ɂ���Ė����n�قȂ�̂ŁC�����n��͖�����ޑ��݂��邱�ƂɂȂ�B
�Q�D�b���O���̏ꍇ
�@�@�@![]()
�����ŁC
�������|���C�������|���Ƃ����ƁC
![]()
�����W�J���Ă��ɂ��Đ�������ƁC
![]()
����āC
![]()
![]()
![]()
�����ŁC![]() �Ƃ����C
�Ƃ����C
![]()
![]()
![]()
����萔�Ƃ݂��ꍇ���Ȃ��Ƃ��C
![]()
![]()
![]()
�͏\���傫�����ɑ��Ă����O�C�����O�C�����O�������Ƃ͖��炩�ł���B
�܂��C![]()
![]() �ł���C���C���C���͎O�p���������Ă���B
�ł���C���C���C���͎O�p���������Ă���B
�ȏ���C�s�^�S���X���͖����ɑ��݂��邱�Ƃ������ꂽ�B
�@��̓I�Ȓl�����߂Ă݂悤�B
�B
�����P�̂Ƃ�
�@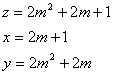
�@�@�����P�Ƃ����
�@�@�����T�C�����R�C�����S
�@�@����āC�i���C���C���j���i�R�C�S�C�T�j
�A�@�����Q�Ƃ����
�@�@�����P�R�C�����T�C�����P�Q
�@����āC�i���C���C���j���i�T�C�P�Q�C�P�R�j
�B�@�����R�Ƃ���ƁC
�@�@�����Q�T�C�����V�C�����Q�S
�@�@����āC�i���C���C���j���i�V�C�Q�S�C�Q�T�j
�C�@�����S�Ƃ���ƁC
�@�@�����S�P�C�����X�C�����S�O
�@�@����āC�i���C���C���j���i�X�C�S�O�C�S�P�j
�D�@�����T�Ƃ���ƁC
�@�@�����U�P�C�����P�P�C�����U�O
�@�@����āC�i���C���C���j���i�P�P�C�U�O�C�U�P�j
�E�@�����U�Ƃ���ƁC
�@�@�����W�T�C�����P�R�C�����W�S
�@�@����āC�i���C���C���j���i�P�R�C�W�S�C�W�T�j
�C
�����Q�̂Ƃ�
�@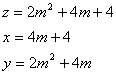
�@�@�����P�Ƃ���ƁC
�@�@�����P�O�C�����W�C�����U
�@�@����āC�i���C���C���j���i�S�C�R�C�T�j
�A�@�����Q�Ƃ���ƁC
�@�@�����Q�O�C�����P�Q�C�����P�U
�@�@����āC�i���C���C���j���i�R�C�S�C�T�j
�B �����R�Ƃ���ƁC
�@�@�����R�S�C�����P�U�C�����R�O
�@�@����āC�i���C���C���j���i�W�C�P�T�C�P�V�j
�C�@�����S�Ƃ���ƁC
�@�@�����T�Q�C�����Q�O�C�����S�W
�@�@����āC�i���C���C���j���i�T�C�P�Q�C�P�R�j
�D�@�����T�Ƃ���ƁC
�@�@�����V�S�C�����Q�S�C�����V�O
�@�@����āC�i���C���C���j���i�P�Q�C�R�T�C�R�V�j
�E�@�����U�Ƃ���ƁC
�@�@�����P�O�O�C�����Q�W�C�����X�U
�@�@����āC�i���C���C���j���i�V�C�Q�S�C�Q�T�j
�A
�ƇA�͏d�������邪�C���炩�ɈႤ�����n������o���Ă���B���̒l�ɂ���Ė����n�قȂ�̂ŁC�����n��͖�����ޑ��݂��邱�ƂɂȂ�B
�R�D�b���P�Q�O���̏ꍇ
�@�@�@![]()
�����ŁC
�������|���C�������|���Ƃ����ƁC
![]()
�����W�J���Ă��ɂ��Đ�������ƁC
![]()
����͂b���U�O���̏ꍇ�ƑS���������ł���B
�ȉ��̋c�_���قƂ�Ǔ����ɂȂ邪�C���̒u����������Ă���̂Ŏ�قȂ�B
�����ŁC���{�����O�̂Ƃ��C�����O�܂��̓����O�ł��邪�C�����O�Ƃ���Ƃ����|���ƂȂ�C���C�������̗L�����ł���Ƃ�������ɔ�����B�����O�Ƃ���ƁC�������ƂȂ�b�ƒ�p�Ƃ���Q���ӎO�p�`�ɂȂ邪�C����͂b���P�Q�O���ɔ�����B����āC���{�����O
���������āC
![]()
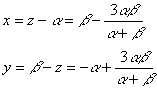 �@�@�@�@�@�@
�@�@�@�@�@�@
�@�@�ȉ����@�͂Q����B��́C�b���U�O���̏ꍇ�P������@�i�T�j�ł���C������͕��ꃿ�{�����ɂ���ď�����悤�ɂ��Ă����@�i�U�j�ł���B
�T�@�b���U�O���̏ꍇ�P������@
���ꂼ��̗��ӂɃ��{����������ƁC
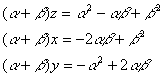 �@�@�@�@�@�@�`
�@�@�@�@�@�@�`
![]()
�i���{���j���C�i���{���j���C�i���{���j�������ꂼ��C���C���C���ƒu�������ƁC
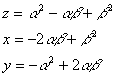
�����O�C�����O�C�����O�̏�����������O�Ȃ�O���������^�Q�ł���C�����O�Ȃ���^�Q�������O
���������āC
![]()
�ƂȂ�C���C���C���͎O�p���������Ă���B�����O�ł���̂ŁC���̗L�������i���C���C���j�͖����ɑ��݂��邱�Ƃ��Ȃ킿���R�����i���C���C���j�͖����ɑ��݂��邱�Ƃ������ꂽ�B
�U�@���ꃿ�{�����ɂ���ď�����悤�ɂ��Ă����@
![]() �i���C���C���͓K���ȗL�����j�Ƃ����āC���ꂪ������悤�ɂ��C���C���̒l�����߂�B�`�̎��ɑ������ƁC
�i���C���C���͓K���ȗL�����j�Ƃ����āC���ꂪ������悤�ɂ��C���C���̒l�����߂�B�`�̎��ɑ������ƁC
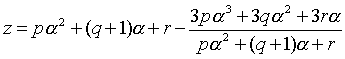
�㔼�̂��Z![]()
![]() �����s����ƁC����
�����s����ƁC����![]() �ŗ]�肪
�ŗ]�肪![]() �ł���B����āC�����邽�߂̏����́C�����|�P�C�����O�ł���B���̂Ƃ��C
�ł���B����āC�����邽�߂̏����́C�����|�P�C�����O�ł���B���̂Ƃ��C
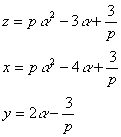
���ӂ����{���āA���ꂼ������߂Ă��A���A���Ƃ�����
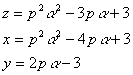
����āC�����O�̂Ƃ��͏\���傫�����ɑ��Ă����O�C�����O�C�����O�ł���A�����O�̂Ƃ��͏\�����������ɑ��Ă����O�C�����O�C�����O�ł���B
�@�܂��C
![]()
���C�����O�̂Ƃ��͏\���傫�����ɑ��Ă��{���|�����O�ł���A�����O�̂Ƃ��͏\�����������ɑ��Ă��{���|�����O�����C���C���C���͎O�p���������Ă���B
�@�ȏ��莩�R�����i���C���C���j�͖����ɑ��݂��Ă��邱�Ƃ������ꂽ�B�������̉��������Ă݂悤�B
�D
�����P�̂Ƃ�
�@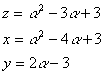
�@�@�����S�Ƃ����
�@�@�����V�C�����R�C�����T
����āC�i�R�C�T�C�V�j
�A�@�����T�Ƃ����
�@�@�����P�R�C�����W�C�����V
�@����āC�i���C���C���j���i�W�C�V�C�P�R�j
�B�@�����U�Ƃ���ƁC
�@�@�����Q�P�C�����P�T�C�����X
�@�@����āC�i���C���C���j���i�T�C�R�C�V�j
�C�@�����V�Ƃ���ƁC
�@�@�����R�P�C�����Q�S�C�����P�P
�@�@����āC�i���C���C���j���i�Q�S�C�P�P�C�R�P�j
�D�@�����W�Ƃ���ƁC
�@�@�����S�R�C�����R�T�C�����P�R
�@�@����āC�i���C���C���j���i�R�T�C�P�R�C�S�R�j
�E�@�����X�Ƃ���ƁC
�@�@�����T�V�C�����S�W�C�����P�T
�@�@����āC�i���C���C���j���i�P�U�C�T�C�P�X�j
�E
�����Q�̂Ƃ�
�@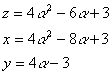
�@�@�����R�Ƃ���ƁC
�@�@�����Q�P�C�����P�T�C�����X
�@�@����āC�i���C���C���j���i�T�C�R�C�V�j
�A�@�����S�Ƃ���ƁC
�@�@�����S�R�C�����R�T�C�����P�R
�@�@����āC�i���C���C���j���i�R�T�C�P�R�C�S�R�j
�B �����T�Ƃ���ƁC
�@�@�����V�R�C�����U�R�C�����P�V
�@�@����āC�i���C���C���j���i�U�R�C�P�V�C�V�R�j
�C�@�����U�Ƃ���ƁC
�@�@�����P�P�P�C�����X�X�C�����Q�P
�@�@����āC�i���C���C���j���i�R�R�C�V�C�R�V�j
�D�@�����V�Ƃ���ƁC
�@�@�����P�T�V�C�����P�S�R�C�����Q�T
�@�@����āC�i���C���C���j���i�P�S�R�C�Q�T�C�P�T�V�j
�E�@�����W�Ƃ���ƁC
�@�@�����Q�P�P�C�����P�X�T�C�����Q�X
�@�@����āC�i���C���C���j���i�P�X�T�C�Q�X�C�Q�P�P�j
�@
�A�͏d�������邪�C���炩�ɈႤ�����n������o���Ă���B���̒l�ɂ���Ė����n�قȂ�̂ŁC�����n��͖�����ޑ��݂��邱�ƂɂȂ�B
�S�D�����P�^�Q�C�����O�C�|�P�������P�̏ꍇ
�@�@�@![]()
�����ŁC
�������|���C�������|���Ƃ����ƁC
![]()
�����W�J���Ă��ɂ��Đ�������ƁC
![]()
����āC�����P�^�Q�Ȃ��
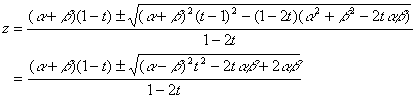 �`
�`
���̂悤�ȕ��G�Ȏ����烋�[�g�������C�������ɂ���ĕ���������Ă��܂����̂Ȃ̂��낤���H
�����|�P�^�Q�̏ꍇ���肪������ɂ��Ă݂悤�B
�����|�P�^�Q�Ƃ����ƁC
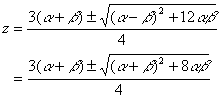 �@�@�@�@�a
�@�@�@�@�a
�U���ꃿ�{�����ɂ���ď�����悤�ɂ��Ă����@�ł͔C�ӂ̐������ɑ��āC
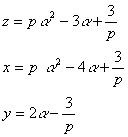
�ł������B���̂Ƃ��C
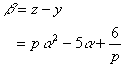
��������a�ɑ������ƁC
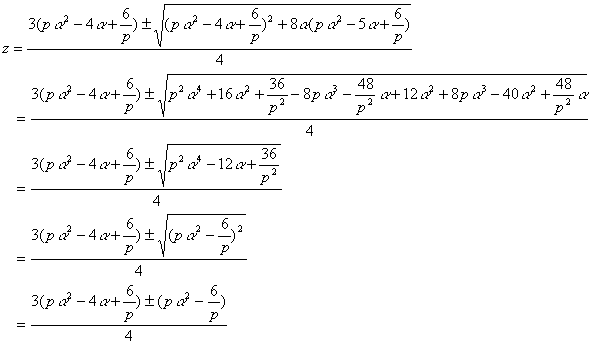
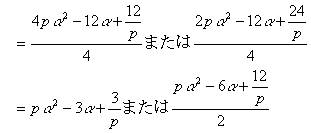
���@�̂悤�Ƀ��[�g���͂���C����������̏ꍇ�͕���܂ŏ����Ă���I�I�I
�ǂ����|�C���g�́C�������̂Q�����ɒu�����Ƃɂ���悤�ł���B
![]()
�ɂ����āC
![]()
�Ƃ����Ă݂悤�B����ɁC���[�g�̒����c�Ƃ����ƁC
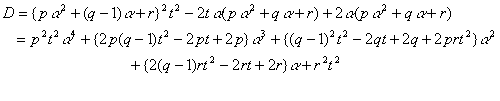 �����ŁC
�����ŁC
![]()
![]() ���O
���O
�Ƃ����ƁC
![]()
�ł���C
![]() �@�@�@
�@�@�@
�����ŁC
![]()
�Ƃ����ƁC
![]()
�ł���C���b�����S�����ɂȂ邽�߂̏����́C
![]()
���Ȃ킿�C
![]()
![]() ���C
���C
![]()
���Ȃ킿�C
![]()
���̂Ƃ��C
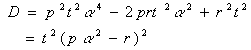
���������āC
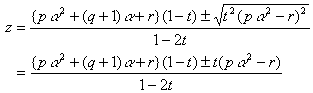
����āC�����
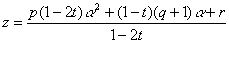
�����ŁC![]() ��������ƁC
��������ƁC
![]()
�������|���C�������|�����
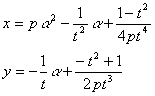
�䂦�ɁC�����O�̂Ƃ��͏\�����������ɑ��āC�����O�̂Ƃ��͏\���傫�����ɑ��āC�����O�C�����O�C�����O�����C�ő�ӂ͂��܂��͂��ł���B�������C
�@�@�b���|���b���b���b����
���������āC���C���C���͎O�p���������B
�ȏ���C���̗L�������i���C���C���j�͖����ɑ��݂���B���Ȃ킿�C���R�����i���C���C���j�������ɑ��݂���B
�����P�^�R�C�|�R�^�V�ɂ��Ă������̉��������Ă݂悤�B
�@�����P�^�R�̂Ƃ�
�����P�̏ꍇ
�@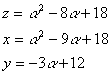
�@�@�����Q�Ƃ����
�@�@�����U�C�����S�C�����U
����āC�i���C���C���j���i�Q�C�R�C�R�j
�A�@�����P�Ƃ����
�@�@�����P�P�C�����P�O�C�����X
�@����āC�i���C���C���j���i�P�O�C�X�C�P�P�j
�B�@�����O�Ƃ���ƁC
�@�@�����P�W�C�����P�W�C�����P�Q
�@�@����āC�i���C���C���j���i�R�C�Q�C�R�j
�C�@�����|�P�Ƃ���ƁC
�@�@�����Q�V�C�����Q�W�C�����P�T
�@�@����āC�i���C���C���j���i�Q�W�C�P�T�C�Q�V�j
�D�@�����|�Q�Ƃ���ƁC
�@�@�����R�W�C�����S�O�C�����P�W
�@�@����āC�i���C���C���j���i�Q�O�C�X�C�P�X�j
�E�@�����|�R�Ƃ���ƁC
�@�@�����T�P�C�����T�S�C�����Q�P
�@�@����āC�i���C���C���j���i�P�W�C�V�C�P�V�j
�����Q�̂Ƃ�
�@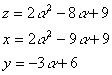
�@�@�����P�Ƃ���ƁC
�@�@�����R�C�����Q�C�����R
�@�@����āC�i���C���C���j���i�Q�C�R�C�R�j
�A�@�����O�Ƃ���ƁC
�@�@�����X�C�����X�C�����U
�@�@����āC�i���C���C���j���i�R�C�Q�C�R�j
�B �����|�P�Ƃ���ƁC
�@�@�����P�X�C�����Q�O�C�����X
�@�@����āC�i���C���C���j���i�Q�O�C�X�C�P�X�j
�C�@�����|�Q�Ƃ���ƁC
�@�@�����R�R�C�����R�T�C�����P�Q
�@�@����āC�i���C���C���j���i�R�T�C�P�Q�C�R�R�j
�D�@�����|�R�Ƃ���ƁC
�@�@�����T�P�C�����T�S�C�����P�T
�@�@����āC�i���C���C���j���i�P�W�C�T�C�P�V�j
�E�@�����|�S�Ƃ���ƁC
�@�@�����V�R�C�����P�W�C�����V�R
�@�@����āC�i���C���C���j���i�V�V�C�Q�X�C�V�R�j
�@�A�͏d�������邪�C���炩�ɈႤ�����n������o���Ă���B���̒l�ɂ���Ė����n�قȂ�̂ŁC�����n��͖�����ޑ��݂��邱�ƂɂȂ�B
�����|�R�^�V�̂Ƃ�
�����P�Ƃ���B
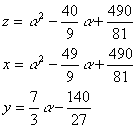
���ׂĂ̗��ӂɂW�P�������āC���߂Ă��C���C���Ƃ����ƁC
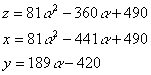
�@�@�����S�Ƃ���ƁC
�@�@�����R�S�U�C�����Q�Q�C�����R�R�U
�@�@����āC�i���C���C���j���i�P�P�C�P�U�W�C�P�V�R�j
�A�@�����T�Ƃ���ƁC
�@�@�����V�P�T�C�����R�P�O�C�����T�Q�T
�@�@����āC�i���C���C���j���i�U�Q�C�P�O�T�C�P�S�R�j
�B �����U�Ƃ���ƁC
�@�@�����P�Q�S�U�C�����V�U�O�C�����V�P�S
�@�@����āC�i���C���C���j���i�R�W�O�C�R�T�V�C�U�Q�R�j
���g��s�^�S���X�����
���C���C����L�����Ƃ���Ƃ��A
![]()
�́A�������i���R�������܂ށj�����ł��낤���B�]���藝�ɂ����鎩�R������i�g������������j���肪����ɁA���̖����l���Ă݂悤�B�g����������ł́A����}��ϐ����̈ꎟ���ŁA���̓�̓��̓��ƂȂ����B
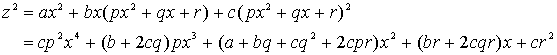 �@�����ŁA
�@�����ŁA![]() �Ƃ����Ă݂悤�B����ƁA
�Ƃ����Ă݂悤�B����ƁA
���ꂪ�A���S�����ɂȂ�悤�ɁA
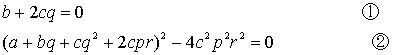
�Ƃ����B�����![]() �A
�A
![]()
������![]() �Ƃ����A
�Ƃ����A
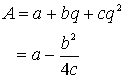
�܂��A�A����
![]()
���Ȃ킿�A
![]()
![]()
����āA![]() �Ȃ��
�Ȃ��
![]() ���Ȃ킿�A
���Ȃ킿�A
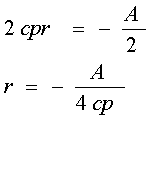
���������āA
![]()
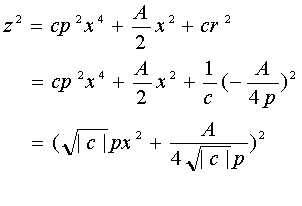 �䂦�ɁA
�䂦�ɁA
����āA�����O�C�����O�C�����O�i���̗L�����j�Ɍ��肷��ƁA
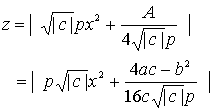
�\���傫�����܂��͏\�����������ɑ���
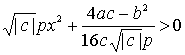
��������A
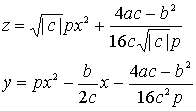
�����O�Ƃ��ė��ӂ�![]() �������āA
�������āA
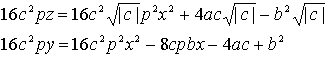
����āA![]() �ł����������Ȃ��
�ł����������Ȃ��
![]() ��
��
![]()
�̐��̗L�������ł���A���ₘ�ɉ����Ė����ɑ��݂���B�����āA![]() �̕���̌��{����������A���R�����ƂȂ�̂ŁA���R�����͖����ɑ��݂���B
�̕���̌��{����������A���R�����ƂȂ�̂ŁA���R�����͖����ɑ��݂���B
����ł͂������̎��R�������������Ƃɂ��悤�B
�T�@�����Q�C�����R�C�����P�̂Ƃ�
�@![]()
�����P�Ƃ����
�@![]()
�@
�����Q�̂Ƃ��A�i�R�Q�C�P�V�C�U�R�j
�A
�����R�̂Ƃ��A�i�S�W�C�V�R�C�P�S�R�j
�B
�����S�̂Ƃ��A�i�U�S�C�P�U�P�C�Q�T�T�j
�C
�����T�̂Ƃ��A�i�W�O�C�Q�W�P�C�R�X�X�j
�D
�����U�̂Ƃ��A�i�X�U�C�S�R�R�C�T�V�T�j
�����Q�Ƃ���ƁA
![]()
�@
�����R�̂Ƃ��A�i�X�U�C�S�R�R�C�T�V�T�j
�A
�����S�̂Ƃ��A�i�P�Q�W�C�W�R�R�C�P�O�Q�R�j
�B
�����T�̂Ƃ��A�i�P�U�O�C�P�R�U�P�C�P�T�X�X�j
�C
�����U�̂Ƃ��A�i�P�X�Q�C�Q�O�P�V�C�Q�R�O�R�j
�D
�����V�̂Ƃ��A�i�Q�Q�S�C�Q�W�O�P�C�R�P�R�T�j
�U�@�����|�Q�C�����T�C�����P�̂Ƃ�
![]()
�����P�̂Ƃ�
![]()
�@
�����Q�̂Ƃ��A�i�R�Q�C�P�V�C�R�P�j
�A
�����R�̂Ƃ��A�i�S�W�C�T�V�C�P�P�P�j
�B
�����S�̂Ƃ��A�i�U�S�C�P�Q�X�C�Q�Q�R�j
�C
�����T�̂Ƃ��A�i�W�O�C�Q�R�R�C�R�U�V�j
�D
�����U�̂Ƃ��A�i�X�U�C�R�U�X�C�T�S�R�j
�����Q�̂Ƃ��A
![]()
�@
�����P�̂Ƃ��A�i�R�Q�C�P�V�C�R�P�j
�A
�����Q�̂Ƃ��A�i�U�S�C�P�Q�X�C�Q�Q�R�j
�B
�����R�̂Ƃ��A�i�X�U�C�R�U�X�C�T�S�R�j
�C
�����S�̂Ƃ��A�i�P�Q�W�C�V�R�V�C�X�X�P�j
�D
�����T�̂Ƃ��A�i�P�U�O�C�P�Q�R�R�C�P�T�U�V�j
�V�@�����R�C�����|�P�C�����S�̂Ƃ��A
![]()
�����P�Ƃ���ƁA
![]()
�@
�����P�̂Ƃ��A�i�Q�T�U�C�Q�S�P�C�U�O�U�j
�A
�����Q�̂Ƃ��A�i�T�P�Q�C�P�O�S�P�C�Q�P�S�Q�j
�B
�����R�̂Ƃ��A�i�V�U�W�C�Q�R�T�R�C�S�V�O�Q�j
�O�y�[�W�ɂ����ẮA![]() �̏ꍇ�ɂ��čl�����B���̃y�[�W�ł́A
�̏ꍇ�ɂ��čl�����B���̃y�[�W�ł́A![]() �̏ꍇ�ɂ��čl���邱�Ƃɂ��悤�B
�̏ꍇ�ɂ��čl���邱�Ƃɂ��悤�B
![]()
�̗��ӂ������O�Ƃ��Ă��Ŋ���ƁA
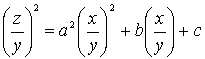
�����ŁA![]() �C
�C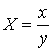 �Ƃ����ƁA
�Ƃ����ƁA
![]()
![]() �����肵�Ă���̂ŁA
�����肵�Ă���̂ŁA
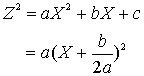
�����O�Ƃ���ƁA
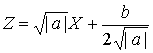
�y�C�w�����ɖ߂��āA
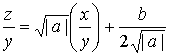
���ӂɂ���������ƁA
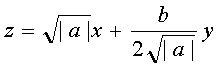
�䂦�ɁA�����������Ȃ�ΓK���Ȏ��R�����C���ɂ��āA���͎��R���ł���B����āA![]() �̎��R����
�̎��R����![]() �͖����ɑ��݂���B�Ȃ��A�����������ł���ꍇ
�͖����ɑ��݂���B�Ȃ��A�����������ł���ꍇ![]() ���炃���������ł���B
���炃���������ł���B
�@���R�����̂������������Ă݂悤�B
�����S�C�����P�Q�C�����X�̂Ƃ��A
![]()
�̉��́C![]() �ł���A
�ł���A
�@
�����P�C�����P�̂Ƃ��A�i�P�C�P�C�T�j
�A
�����Q�C�����R�̂Ƃ��A�i�Q�C�R�C�P�R�j
�B
�����R�C�����Q�̂Ƃ��A�i�R�C�Q�C�P�Q�j
�C
�����S�C�����T�̂Ƃ��A�i�S�C�T�C�Q�R�j
![]() ��L�����Ƃ���Ƃ��A
��L�����Ƃ���Ƃ��A
������
![]() �@�@�@�@�@�@�`
�@�@�@�@�@�@�`
�͎��R�����������B
����̏����̂Ƃ��A���R�����������Ȃ����Ƃ͏ؖ�����Ă���B����̏����Ƃ́A
�����R�ŁA![]() �̂Ƃ��ŁA
�̂Ƃ��ŁA
![]()
�ł���B���Ȃ킿�A�L���ȃt�F���}�[�̒藝�ł���B
�@���`�͏�Ɏ��R�����������Ȃ����낤���B�����Q�̂Ƃ��́A
![]()
�ɂ����āA���܂��͂����������Ȃ�A���R�����������ɑ��݂��邱�Ƃ́A���łɂ��̂g�o��ŏؖ�����Ă���B
�@�����R�̂Ƃ��͂ǂ��ł��낤���B���̏ꍇ�A���R�����������ɑ��݂��邱�Ƃ͎����ł���B���C�������R���Ƃ��A
![]()
![]()
![]()
�ƂȂ�Ƃ��ł���B���̏ꍇ�A���`�͎��̂悤�Ɉ������������B
![]()
����āA�i���C���C�����{�����j�͎��`�̎��R�����ł���B���C���͔C�ӂ̎��R�����Ƃ邱�Ƃ��ł���̂ŁA���`�̎��R�����͖����ɑ��݂���B
�@���ꂩ��̌����ۑ�́A�����Ȃ�Ƃ��Ɏ��`�͖����Ɏ��R���������̂��A�܂��͂����Ȃ��̂��ł���B
�@�Ȃ��A��A�������������Ƃ������ƂƗL�������������Ƃ͓��l�ł���B�Ȃ��Ȃ�L������![]() �����݂����Ƃ���ƁA
�����݂����Ƃ���ƁA![]() �̕���̌��{�����ɂ���āA
�̕���̌��{�����ɂ���āA![]() �͐����̑g�ł��邪�A
�͐����̑g�ł��邪�A![]() �̂Ƃ��A
�̂Ƃ��A
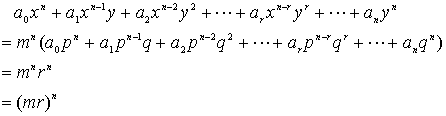
�̌v�Z����![]() ����A�̉��ł��邩��ł���B
����A�̉��ł��邩��ł���B
�@���l��![]() ���L�������̂Ƃ��A�C�ӂ̗L��������������
���L�������̂Ƃ��A�C�ӂ̗L��������������![]() �����`�̉��ł���B������ʂ̉��Ƃ���ƁA���͑��݂���Ƃ���Ώ�ɖ����ɂ��邱�ƂɂȂ��Ă��܂��̂ŁA�����ł�
�����`�̉��ł���B������ʂ̉��Ƃ���ƁA���͑��݂���Ƃ���Ώ�ɖ����ɂ��邱�ƂɂȂ��Ă��܂��̂ŁA�����ł�![]() �̂Ƃ��A��
�̂Ƃ��A��![]() �Ɖ�
�Ɖ�![]() ����ƒ�`���邱�Ƃɂ���B���������āA�قȂ���̒�`�́A
����ƒ�`���邱�Ƃɂ���B���������āA�قȂ���̒�`�́A![]() �ƂȂ邱�Ƃł���B
�ƂȂ邱�Ƃł���B
�g��t�F���}�[�\�z
������
![]()
�͂����Q�̏ꍇ���܂߂���������ł͎��R��������������Ȃ��B
�@�@ �T�@�����Q�̏ꍇ
�T�@�����Q�i�Q���j�̏ꍇ
������
![]()
��![]() �܂���
�܂���![]() ���L�����̕������ł���Ƃ��A���R�������ɂ����Ă��邱�Ƃ́A���̃T�C�g��ł��łɏؖ�����Ă����i���g��s�^�S���X�����Q�Ɓj�B����āA������
���L�����̕������ł���Ƃ��A���R�������ɂ����Ă��邱�Ƃ́A���̃T�C�g��ł��łɏؖ�����Ă����i���g��s�^�S���X�����Q�Ɓj�B����āA������![]() �����������Ȃ����߂̕K�v�����́A
�����������Ȃ����߂̕K�v�����́A![]() �C
�C![]() �̗������L�����̕������łȂ����Ƃł���B�ł́A����ŏ\���ł��낤���B�\�������łȂ����Ƃ́A���̔��Ⴉ�疾�炩�ł���B
�̗������L�����̕������łȂ����Ƃł���B�ł́A����ŏ\���ł��낤���B�\�������łȂ����Ƃ́A���̔��Ⴉ�疾�炩�ł���B
�@������![]() ��
��![]() �Ȃlj��������Ă���B
�Ȃlj��������Ă���B![]() �C
�C![]() �̗������L�����̕������łȂ��̂ɉ�������͂��̑�������ł��o�����Ƃ��ł���B������
�̗������L�����̕������łȂ��̂ɉ�������͂��̑�������ł��o�����Ƃ��ł���B������![]() �́A
�́A![]() ���A������
���A������![]() �́A
�́A![]() �����Ƃ��Ă��ȂǁB
�����Ƃ��Ă��ȂǁB
�@������![]() �����������Ȃ����߂̕K�v�\�������͉��Ȃ̂��B��̓I�ȏꍇ���������āA�肪����邱�Ƃɂ��悤�B
�����������Ȃ����߂̕K�v�\�������͉��Ȃ̂��B��̓I�ȏꍇ���������āA�肪����邱�Ƃɂ��悤�B
�@�@![]()
�A�@![]()
�B�@![]() �ɂ����āA
�ɂ����āA![]() �̗������L�����̕������łȂ��̂ɁA����������
�̗������L�����̕������łȂ��̂ɁA����������
�C�@![]() �͉�������݂���Ȃ�A�����ɂ����B
�͉�������݂���Ȃ�A�����ɂ����B
�@�@������![]() �͎��R��������������Ȃ����Ƃ̏ؖ�
�͎��R��������������Ȃ����Ƃ̏ؖ�
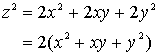
���R���������Ɖ��肷��B
A)
���C����������ł���Ƃ���ƁA![]() �͊�ł���B����āA
�͊�ł���B����āA![]() �͖������ƂȂ��Ė�������B
�͖������ƂȂ��Ė�������B
B)
�������A�����������ł���Ƃ���ƁA![]() �͊�ƂȂ�A
�͊�ƂȂ�A![]() �͖������ƂȂ��Ė�������B
�͖������ƂȂ��Ė�������B
C)
���������ł���Ƃ���ƁA���C���̍ő�����ɂ����![]() �Ƃ�����B���̂Ƃ��A
�Ƃ�����B���̂Ƃ��A![]() �ƂȂ�
�ƂȂ�![]() �͖������ƂȂ��Ė�������B
�͖������ƂȂ��Ė�������B
A)B)C)���![]() �͎��R�����������Ȃ��B
�͎��R�����������Ȃ��B
�����![]() ���A
���A![]() �����R�����������Ȃ��B
�����R�����������Ȃ��B
�A�@![]() �͎��R�����������Ȃ����Ƃ̏ؖ�
�͎��R�����������Ȃ����Ƃ̏ؖ�
������![]() �����R���������Ɖ��肷��B
�����R���������Ɖ��肷��B
![]() �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�`
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�`
��ό`�����
![]() �@�@�@�@�@�@�@�@ �@�@ �a
�@�@�@�@�@�@�@�@ �@�@ �a
�T�@���A���̗�������ł���ꍇ
���`���A������B�����ŁA![]()
�Ƃ����ƁA�a���
![]()
����āA
![]()
![]() �̗�������܂��͋����Ƃ���ƁA
�̗�������܂��͋����Ƃ���ƁA![]() �������A
�������A![]() �̈������ő����������ł���Ƃ���ƁA
�̈������ő����������ł���Ƃ���ƁA![]() �������ƂȂ�A�E�ӂ���ł��邱�Ƃɔ�����B
�������ƂȂ�A�E�ӂ���ł��邱�Ƃɔ�����B
�U�@������ŁA���������ł���ꍇ
�`��肚�͋����ł���B����āA���{�������|���������ƂȂ�A���a�̍��ӂ͂S�̔{���ł���B�Ƃ��낪�A![]() �͊�ŁA���ӂ��Q�Ŋ���ƍ��ӂ͋����A�E�ӂ͊�ƂȂ��Ė�������B
�͊�ŁA���ӂ��Q�Ŋ���ƍ��ӂ͋����A�E�ӂ͊�ƂȂ��Ė�������B
�V�@���������ŁA������ł���ꍇ
���`���A���͊�ł���B����āA���{�������|���������ƂȂ�A���a�̍��ӂ͂S�̔{���ł���B�Ƃ��낪�A![]() �͊�ŁA���ӂ��Q�Ŋ���ƍ��ӂ͋����A�E�ӂ͊�ƂȂ��Ė�������B
�͊�ŁA���ӂ��Q�Ŋ���ƍ��ӂ͋����A�E�ӂ͊�ƂȂ��Ė�������B
�W�@���A�����ɋ����ł���ꍇ
���`���炚�������ł���B���A���A���̍ő�������Ƃ��A![]() �Ƃ����ƁA
�Ƃ����ƁA![]() �̏��Ȃ��Ƃ���͊�ł���B���`�ɑ�����Đ�������ƁA
�̏��Ȃ��Ƃ���͊�ł���B���`�ɑ�����Đ�������ƁA
![]()
�䂦�ɁA![]() ������ő��͋����ł��邱�Ƃ͂ł��Ȃ�����A
������ő��͋����ł��邱�Ƃ͂ł��Ȃ�����A![]() �̏��Ȃ��Ƃ�����͊�ł���B���������āA�T�U�V���疵������B
�̏��Ȃ��Ƃ�����͊�ł���B���������āA�T�U�V���疵������B
�ȏ�T�U�V�W���������![]() �͎��R�����������Ȃ����Ƃ��ؖ����ꂽ�B
�͎��R�����������Ȃ����Ƃ��ؖ����ꂽ�B
�B�@![]() �ɂ����āA
�ɂ����āA![]() �̗������L�����̕������łȂ��̂ɁA����������
�̗������L�����̕������łȂ��̂ɁA����������
![]() �@�@�@�@�@�@�@A
�@�@�@�@�@�@�@A
�̗��ӂ�![]() �Ŋ���A
�Ŋ���A![]() �ƒu���ƁA
�ƒu���ƁA
![]() �@�@�@�@�@�@�@�@B
�@�@�@�@�@�@�@�@B
����āA��A���L�������������ƂƎ�B���L�������������Ƃ͓��l�ł��邩��A��A���L�������������߂̕K�v�\�������́A��B���L�����������Ƃł���B���Ȃ킿�A��A��![]() ���L�����̕������ƂȂ�悤�ȗL�����������݂���Ȃ�A�L�����������Ȃ킿���R���������B
���L�����̕������ƂȂ�悤�ȗL�����������݂���Ȃ�A�L�����������Ȃ킿���R���������B
�@��B�ɂ����P��������ƁA
![]()
����āA![]() ���������ł���Ƃ��́A�������B�Ⴆ�A
���������ł���Ƃ��́A�������B�Ⴆ�A![]() ��
��![]() �Ƃ��Ȃǂł���B
�Ƃ��Ȃǂł���B
![]() �C
�C![]()
�O�҂���҂�![]() �����Ƃ��Ď��B�O�҂́A���̂ق�
�����Ƃ��Ď��B�O�҂́A���̂ق�
![]() �Ȃǂ����Ƃ��Ď����A��҂�
�Ȃǂ����Ƃ��Ď����A��҂�![]() �Ȃǂ����Ƃ��Ď��B
�Ȃǂ����Ƃ��Ď��B
�@��B�ɂ����Q��������ƁA
![]()
����āA![]()
![]() ���������Ȃ�A��A�͉������B��́A
���������Ȃ�A��A�͉������B��́A
![]()
![]() �Ȃǂł���B
�Ȃǂł���B
![]()
![]()
![]()
![]()
���ꂼ��̉������Ɉ��������ƁA![]() �ł���B
�ł���B
�A�ɂ�����ؖ�����
![]() �C
�C![]() �C
�C
�͐��̗L����������������Ȃ����Ƃ��킩��B
�@�܂��A�@�ɂ�����ؖ�����
![]()
�����̗L�������������Ȃ��B����������A�C�ӂ̗L�������ɑ��āA![]() �͗L�����̕������ɂȂ�Ȃ��A�Ƃ������Ƃł���B
�͗L�����̕������ɂȂ�Ȃ��A�Ƃ������Ƃł���B
�C�@![]() �͉�������Ƃ��A���͖����ɑ��݂��邩�B
�͉�������Ƃ��A���͖����ɑ��݂��邩�B
�܂���̓I�ȏꍇ�ōl���Ă݂悤�B
![]() �@�@�@�@�@�@�@�@�@�@�@�@�@A
�@�@�@�@�@�@�@�@�@�@�@�@�@A
�͉��i���C���C���j���i�P�C�P�C�R�j�������Ă���B���̂Ƃ�����ꂪ��`����Ӗ��ŁA�قȂ�����Ɏ����Ă���ł��낤���B�����̒�`�ŁA��̉�![]() �C
�C![]() ���قȂ������
���قȂ������
![]()
�ł������B
�@��A�̗��ӂ�![]() �Ŋ���A
�Ŋ���A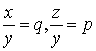 �ƒu���ƁA
�ƒu���ƁA
![]() �@�@�@�@�@B
�@�@�@�@�@B
�o�Ȑ���B�ɗL���_�i���C���j���i�R�C�P�j�����݂��Ă���B�����ŁA�_�i�R�C�P�j��ʂ钼���̌X�������Ƃ���ƁA
![]() �@�@�@�@ C
�@�@�@�@ C
��B�ɑ�����Đ�������ƁA
![]()
���̈�́A�����R�ł���B����āA���̉������Ƃ���ƁA�Q���������̂�������ƌW���̊W����A
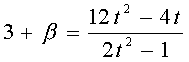
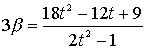
�ł��邪������̏ꍇ���A
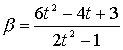
����āA�����L�����ł�����͗L�����ł���B
�������ƒu�������āB
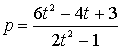
��C�ɑ�����āA
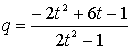
���͔C�ӂ̗L�������Ƃ邱�Ƃ��ł��邩��A�������a�͉�
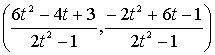
���Ɏ����Ă��邱�Ƃ��ؖ����ꂽ�B
�����P�̂Ƃ��A
�i���C���j���i�T�C�R�j
���̂Ƃ��A�������`�̉���
�i���C���C���j���i�R�C�P�C�T�j
�����Q�̂Ƃ��A
�i���C���j���i�P�X�^�V�C�R�^�V�j
�i���C���C���j���i�R�C�V�C�P�X�j
�����R�^�S�̂Ƃ��A
�i���C���j���i�Q�V�C�P�X�j
�i���C���C���j���i�P�X�C�P�C�Q�V�j
�����S�^�T�̂Ƃ��A
�i���C���j���i�P�R�C�X�j
�i���C���C���j���i�X�C�P�C�P�R�j
�����W�^�P�P�̂Ƃ��A
�i���C���j���i�R�X�T�^�V�C�Q�V�X�^�V�j
�i���C���C���j���i�Q�V�X�C�V�C�R�X�T�j
���Ɉ�ʓI�ɍl���Ă݂悤�B
![]() �@�@�@�@�@�@�a
�@�@�@�@�@�@�a
�ɉ�![]() �����݂���Ɖ��肵�悤�B
�����݂���Ɖ��肵�悤�B
![]() �@�@�@�@�@�c
�@�@�@�@�@�c
�O�Ɠ��l�ɓ_![]() ��ʂ�A�X�������̒������l����ƁA
��ʂ�A�X�������̒������l����ƁA
![]() �@�@�@�@�d
�@�@�@�@�d
���a�ɑ�����Đ�������ƁA
![]()
����̉���![]() �Ȃ̂ŁA�����̉������Ƃ���Ή��ƌW���̊W����
�Ȃ̂ŁA�����̉������Ƃ���Ή��ƌW���̊W����
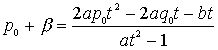 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �e
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �e
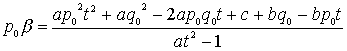 �@�@�@�@�@�@ �f
�@�@�@�@�@�@ �f
���e����
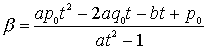
���f����
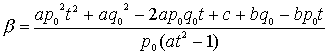
����Ɏ��c���������
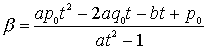
����āA���d������e������������̂��������B
�i�����ł͉��ƌW���̊W�ʼn��������A�Q���������̉��̌����ɑ�����Ă�������B���̂����A���@�̂悤�Ƀ��[�g�������Ă��܂����Ƃ��A�ǎҎ��g�Ŋm�F���Ă������������B�j
�����L�����ł���A���͗L�����B
����āA�C�ӂ̗L�������ɂ��āA
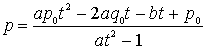
�͕�����![]() ��
��![]() �ȊO�̉��ł���A�����ɑ��݂��邱�Ƃ��킩��B���d�ɑ�����āA
�ȊO�̉��ł���A�����ɑ��݂��邱�Ƃ��킩��B���d�ɑ�����āA
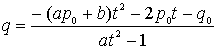
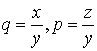 ���A
���A
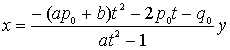
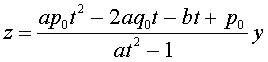
����āA�C�ӂ̗L�������A���ɑ��āA
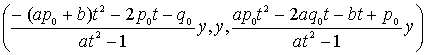
��![]() �̗L�������ł���B�����āA����̌��{����������Ȃ玩�R�����ƂȂ�B
�̗L�������ł���B�����āA����̌��{����������Ȃ玩�R�����ƂȂ�B
�ȏォ��A������![]() �͗L������������Ȃ�A�L�������i����̌��{��������Ȃ玩�R�����j���Ɏ����Ă��邱�Ƃ��ؖ����ꂽ�B����āA������
�͗L������������Ȃ�A�L�������i����̌��{��������Ȃ玩�R�����j���Ɏ����Ă��邱�Ƃ��ؖ����ꂽ�B����āA������![]() �͎��R�������Ɏ����A��������Ȃ����̂ǂ��炩�ł���Ƃ����g��t�F���}�[�\�z�́A�Q���ł͏ؖ����ꂽ���ƂɂȂ�B
�͎��R�������Ɏ����A��������Ȃ����̂ǂ��炩�ł���Ƃ����g��t�F���}�[�\�z�́A�Q���ł͏ؖ����ꂽ���ƂɂȂ�B
�D�@![]() ���肪����Ɏ��R�����i�L�������j�����݂��Ȃ��ꍇ��T���o�����@
���肪����Ɏ��R�����i�L�������j�����݂��Ȃ��ꍇ��T���o�����@
����![]() ���Ŋ���A���^�������A���^�������Ƃ�����
���Ŋ���A���^�������A���^�������Ƃ�����
![]() �@�@�@�@�@�@�@�@�@�`
�@�@�@�@�@�@�@�@�@�`
�����ŁA�������{���Ƃ����ƁA
![]()
���Ȃ킿�A
![]()
���̂Q���������̔��ʎ����c�Ƃ��A�c�^�S�����Ƃ����ƁA
![]()
�����������Ȃ�`�̗L�����������݂��Ă��܂��̂ŁA
![]()
�͗L�������������Ȃ��B����āA
![]()
�͎��R�����i�L�������j����������Ȃ��B
���l�ɂ`�ɂ����āA�������{�Q���Ƃ����ƁA
![]()
�������āA
![]()
�����
�A
![]()
���������āA
![]() �@�@�@�@�@�@�@�@�@�a
�@�@�@�@�@�@�@�@�@�a
![]()
�͎��R��������������Ȃ��B
���a�ɂ����āA�������{���Ƃ����ƁA
![]()
����A
![]()
�䂦�ɁA
![]()
����A
![]()
![]()
�͎��R��������������Ȃ��B
���`�ɂ����āA�������{�����Ƃ����ƁA
![]()
���Ȃ킿�A
![]()
����āA
![]()
���Ȃ킿�A
![]() �@
�@
![]()
�͎��R��������������Ȃ��B
���͔C�ӂ̗L�������Ƃ邱�Ƃ��ł��邩��A���������Ȃ��ꍇ�͖����ɑ��݂��邱�Ƃ��ؖ����ꂽ�B
���l�Ɏ��a�ɂ����āA�������{�����Ƃ����ƁA
![]()
![]()
����āA
![]()
����
![]()
![]()
�P�D
�����Q�Ƃ��A
![]()
![]()
�Q�D
�����R�̂Ƃ�
![]()
![]()
�R�D
�����S�̂Ƃ��A
![]()
![]()
