第9話 数独を解くソフトVer.2の問題点
問題点を探るために、
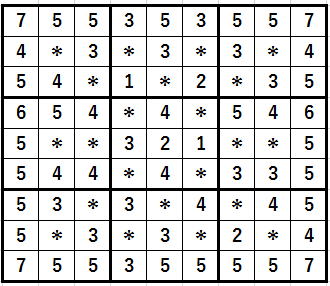
全体リスト構造解析結果を再度見てみましょう。


第4講 数独を解くソフトの開発(1)
第9話 数独を解くソフトVer.2の問題点
問題点を探るために、
全体リスト構造解析結果を再度見てみましょう。



| 1 | 2 | 4 | 5 | 7 | 8 | 9 | 1 | 4 | 5 | 7 | 8 | 1 | 2 | 4 | 5 | 9 | 2 | 6 | 7 | 2 | 3 | 7 | 8 | 9 | 2 | 8 | 9 | 1 | 3 | 4 | 6 | 9 | 1 | 5 | 6 | 8 | 9 | 1 | 3 | 4 | 5 | 6 | 8 | 9 | ||||||||||||||||||||||||||||||||||
| 1 | 2 | 8 | 9 | 1 | 2 | 9 | 2 | 8 | 9 | 1 | 6 | 9 | 1 | 6 | 8 | 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 5 | 7 | 8 | 9 | 4 | 5 | 7 | 8 | 7 | 8 | 9 | 5 | 8 | 9 | 3 | 4 | 5 | 8 | 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 4 | 5 | 6 | 7 | 9 | 1 | 4 | 5 | 6 | 7 | 1 | 4 | 5 | 9 | 2 | 4 | 5 | 7 | 1 | 4 | 6 | 7 | 9 | 1 | 2 | 6 | 9 | 1 | 2 | 4 | 6 | 7 | 9 | |||||||||||||||||||||||||||||||||||||||||||||
| 1 | 4 | 6 | 7 | 9 | 1 | 4 | 7 | 4 | 7 | 1 | 1 | 4 | 6 | 7 | 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 3 | 4 | 5 | 7 | 1 | 4 | 5 | 7 | 1 | 3 | 4 | 5 | 2 | 4 | 5 | 7 | 1 | 4 | 7 | 1 | 2 | 8 | 1 | 2 | 4 | 7 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 4 | 5 | 1 | 2 | 4 | 1 | 2 | 5 | 9 | 1 | 2 | 5 | 9 | 1 | 2 | 3 | 5 | 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 5 | 6 | 8 | 1 | 2 | 5 | 2 | 5 | 8 | 1 | 6 | 1 | 2 | 5 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 1 | 4 | 5 | 6 | 8 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 4 | 2 | 4 | 5 | 8 | 9 | 1 | 2 | 5 | 8 | 9 | 1 | 3 | 6 | 7 | 9 | 1 | 2 | 5 | 6 | 9 | 1 | 2 | 3 | 5 | 6 | 7 | 9 |
| 7 | 5 | 5 | 3 | 5 | 3 | 5 | 5 | 7 |
| 4 | * | 3 | * | 3 | * | 3 | * | 4 |
| 5 | 4 | * | 1 | * | 2 | * | 3 | 5 |
| 6 | 5 | 4 | * | 4 | * | 5 | 4 | 6 |
| 5 | * | * | 3 | 2 | 1 | * | * | 5 |
| 5 | 4 | 4 | * | 4 | * | 3 | 3 | 5 |
| 5 | 3 | * | 3 | * | 4 | * | 4 | 5 |
| 5 | * | 3 | * | 3 | * | 2 | * | 4 |
| 7 | 5 | 5 | 3 | 5 | 5 | 5 | 5 | 7 |
さらに、第3話の探索順
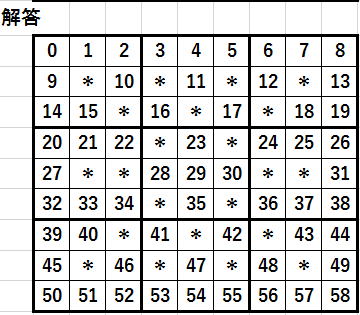
を示しましょう。
何が問題かともしますと最も候補数が多い場合から、
空欄を埋めていっているということです。
本当は、
| 7 | 5 | 5 | 3 | 5 | 3 | 5 | 5 | 7 |
| 4 | * | 3 | * | 3 | * | 3 | * | 4 |
| 5 | 4 | * | 1 | * | 2 | * | 3 | 5 |
| 6 | 5 | 4 | * | 4 | * | 5 | 4 | 6 |
| 5 | * | * | 3 | 2 | 1 | * | * | 5 |
| 5 | 4 | 4 | * | 4 | * | 3 | 3 | 5 |
| 5 | 3 | * | 3 | * | 4 | * | 4 | 5 |
| 5 | * | 3 | * | 3 | * | 2 | * | 4 |
| 7 | 5 | 5 | 3 | 5 | 5 | 5 | 5 | 7 |
本当は色のついているところからはじめるべきです。
これは確定しています。
つまり試行錯誤は必要ありません。
うまくいけば入れたことによって確定セルが出来るかもしれません。
確定セルがなくても各欄の候補数は減るはずです。
解答探索は場合の数が少ないところからはじめるべきです。
例えば、場合の数が2であって、
最初の方に破綻すれば、
約半分の検索量になります。
場合の数が7ならすぐに破綻しても、
探索量は6/7になるだけです。
Ver.1とVer.2のコードに
If mx(y, x) = 0 Then Exit Sub
が入っていますが、これは破綻した場合の処理です。
埋め方によっては、何の数字も入らない場所が発生してしまいます。
これが破綻です。
破綻している場合はそれまでの入れ方に問題があるわけですから、
戻ってやり直すしかないわけです。
試行錯誤法では破綻回数は相当数(千を遙かに超える?)になるはずです。
場合の数の少ないところからはじめると、
すぐに破綻すれば検索量は
1/2化→1/3化→1/2化→・・・
すなわち 1/2×1/3×1/2×・・・となって
次々に減っていくはずです。
場合の数が多い場合には、
6/7×4/5×4/5×・・・
場合の数が少ない場合に比べて減少は圧倒的に少ないですね。
ですから、場合の数が多いところからはじめるより、
場合の数が小さいところからはじめるべきですね。
ですから入力順を変えるだけで35倍加するのは当然といえば当然なのです。
問題によっては、倍加はもっと大きくなるでしょう。
本当のことをいうと 探索順が若いところが、
探索順が若いところが、
場合の数が多くなるように問題を作っていたのです。
つまり、Ver.1とVer.2にとって一番苦手な問題をわざと作ったわけです。
意地悪をしたわけです。
でも相手はソフトですから機嫌を損ねることはないですね。
ということは改善策は「場合の少ないところから入力していくように改良する!」
ということになります。
mx(i, j)が最も少ないところから入力するように変更すればよいのです。
mx(i, j)の最小値を見つけるSubプロシージャnyuryokujyunを作り、
fに引数g(これは入力順を示す)が送られたらfはすぐにそのgをnyuryokujyunに引数にして送ることによって、
入力順をnyuryokujyunに問い合わせればよいのです。
nyuryokujyunの任務はmx(i, j)の最小値の場所を入力場所に選ぶ=そこのy座標iz(g)とx座標 jz(g)を作ってやることです。
では、Ver.3の開発をしてください。
もちろん、空欄を埋めていきますので、影響を受けるセルに色塗りをしていく必要があります。
ですが、影響を受ける部分の部分リスト構造解析は不要です。
なぜなら、毎回
nyuryokujyun (g)
y = iz(g)
x = jz(g)
kyokusyokaiseki y, x
自分が今扱っているセルに対してセルリスト構造解析=局所解析をしてから空欄を埋める作業
For i = 0 To mx(y, x) - 1
m(y, x) = rlst(y, x, i)
をしているからです。
色さえ塗ってあれば、局所解析で正しく解析できます。