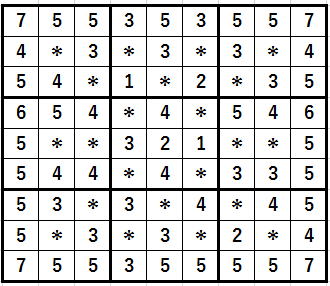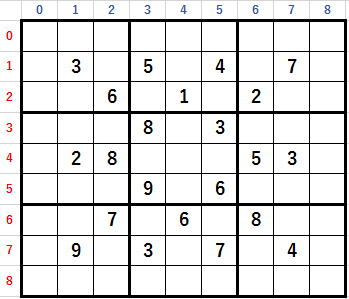
皆さん座標(0, 0)のセルに入る候補をすべて考えてください。
行と列には何もないので、
制約条件はブロックのみです。
3と6のみが禁止されるので、
候補は3と6を除いた1,2,4,5,7,8,9です。
そして可能な数字の候補数は7個です。
このようにセルに入るすべての候補を考えることを、
セルリスト構造解析と私は呼んでいます。
((候補数字集合),候補数字数)をセルリスト構造と定義するからです。
候補数字数は候補数字が何個あるかカウントしたもので、
(候補数字集合)の要素数に等しいですから、
本来は(候補数字集合)の情報の中に含まれていますが、
候補数字数はFor文で制御するときに必要ですので、
重要性を示すために、((1,2,4,5,7,8,9),7)としているわけです。
プログラムを組むときには、グローバル配列
Dim rlst(8, 8, 8) As Byte, mx(8, 8) As Byte
を用意して、候補数字の集合をrlst(i, j, k)に、
候補数字数をmx(i, j)に収納させます。
候補数字の集合を収める配列が3次元になっているのは、
rlst(0, 0, 0)=1,rlst(0, 0, 1)=2,rlst(0, 0, 2)=4,rlst(0, 0, 3)=5,
rlst(0, 0, 4)=7,rlst(0, 0, 5)=8,rlst(0, 0, 6)=9
となるからです。
(※rlstの3番目の添え字の最後はrlst(i, j, mx(i, j) - 1)となることに注意してください。
ですから、For文は
For i =0 To mx(y, x) - 1
となります。)
要するにセル(0, 0)には1,2,4,5,7,8,9と複数あるから、
それらを収納するためには3次元配列にする必要があるのです。
候補数字数は7ですから、
収納するものが1つしかないので2次元配列でよくて、
mx(0, 0)=7
となります。

座標(0,1)のセルならリスト構造は、
((1,4,5,7,8),5)です。
座標(4,4)のセルなら
どうですか。
候補を考えるときにいちいち行のすべての数字、
列のすべての数字、ブロックのすべての数字をチェックしなければならずに、
大変です。
何かうまい方法はないでしょうか。
理詰めで解けるようにするために、
将来ライン排除・ブロック排除・ライン間接排除の機能を付け加えなければなりません。
ライン排除とは、ライン上に数字が入っていることにより、
そのセルを除いたすべてのライン上のセルにその数字が入る可能性を排除する事態を指しています。
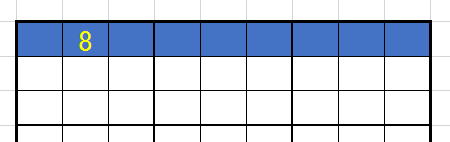
色が塗ってあるところには、8が入りませんね。
このライン排除は数独を解いていく上で最も破壊力を発揮するものです。
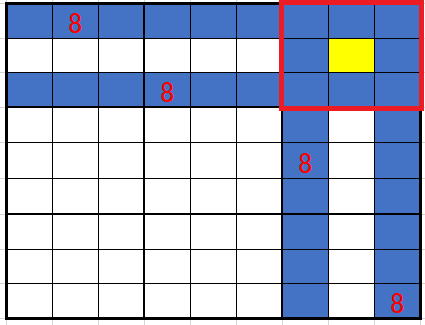
赤いブロックに注目してください。
黄色以外のセルはライン排除によって8の入る可能性が排除されています。
ということは8が入る場所は黄色のセルしかありませんね。
初心者はセルに入る候補の探索=セルリスト構造解析から始めようとしますが、
ヒント数が少ない数独ではこれで決まるセルは基本的には皆無です。
理詰めで解くとは、
確定するセルに確定した数字を埋めていく作業の連続によって解いていくことです。
局面によってはセルに入る候補の探索=セルリスト構造解析によって、
欄に入る数字が確定する場合があります。
これは、候補数字数が1個のときです。
候補数字数が複数のときに、いずれかを仮定する方法を、
ナンプレファンは邪道な方法と見なしますし、
ミスの原因となります。
候補数字数が1個になるのは基本的には中盤から終盤にかけてしか登場しません。
(今回の問題は最初に2カ所ありますが。)
最初はライン排除などによって出来るだけ欄を埋めていき、
中盤以降ではじめてセルに入る候補の探索=セルリスト構造解析をすべきなのです。
ライン排除を私はどのようにして組み込んだかと申しますと、
 色塗りです。
色塗りです。それぞれの数字で排除する色を塗り分けて、
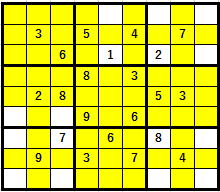
(3を入れては行けない場所を黄色で塗ってあります。ブロック排除もしてあります。
3の確定するセル=空欄がありますね。)
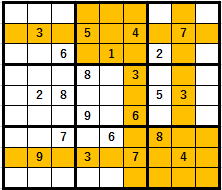
(4を入れてはいけないセル)
このようにすべての数字ごとに色を塗り分けていきます。
すると上のようなシートが基本は9枚できます。
基本と入れたのはすべての数字がヒントにない場合もあるからです。
この作業をすることによって、
ライン排除とブロック排除によって決定できるセルが解明できます。
数独自動生成ソフトの開発にとって跳躍点の1つとなったのが、
色塗りのアイデアでした。
ライン排除だけでなくセルリスト構造解析にも色は使えます。
1つのセルについて、9枚のシートを確認して、
白であるもののみをリストすればよいのです。
Dim ironuri(8, 8, 8) As Byte, rlst(8, 8, 8) As Byte, mx(8, 8) As Byte
ですから、もう一つグローバル配列を用意する必要があります。
そして、Subプロシージャdainyuの最初に、
すべて白に初期化しておきます。
私は、白の場合は0、色が塗ってある場合には1としています。
rlst(i, j, k)と同様に3次元配列にしてある理由は、
ironuri(i, j, k)
kが色の種類(=数字-1)に対応しているからです。
要素数が8ですから、9つの色すなわち9つの数字に対応していますね。
全体リスト構造解析はすべてのセルについて行うだけです。
また、部分構造解析は、
問題を解いていく過程で空欄に数字を入れたことによって影響を受けるセルのみについて、
解析をします。
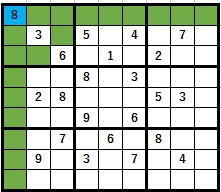
(今回の色は色塗りの色ではなくセルリスト構造解析をするべきセルを示しています。)
3と6の色が抜いてあるのは、
リスト構造解析は空欄のみについて行うべきだからです。
ただし、部分構造解析は不要です。
理由は、第9話で述べます。
では、まずSubプロシージャdainyuで、
最初に色塗りをして、
最後に全体構造解析(空欄に対する全セルリスト構造解析)をやってください。
本当は色のあるところだけをセルリスト構造解析だけをやればよいのですが、
dainyuは再帰的に使うプロシージャf(g)と違い1回しか処理しませんので、
全セルについてリスト構造解析をやっても影響は0に近いと言えます。
なお、セルリスト構造解析はkyokusyokaisekiというSubプロシージャでやって下さい。
セルリスト構造解析をSubプロシージャに独立させておかないと、
コードが複雑になり頭が混乱します。
kyokusyokaisekiの引数はセルの座標にしてください。
ですから、
kyokusyokaiseki i, j
とします。
全体セルリスト構造解析がうまくいっているかを確認するために、
f (0) '数独作成プロシージャ
と
Cells(4, 12) = "問題を解くのにかかった時間は"
Cells(5, 12) = ow - hj
Cells(6, 12) = "秒です。"
If cn = 1 And seigohantei = 1 Then Cells(7, 12) = "正しい解答です。" Else Cells(7, 12) = "誤った解答です。"
は注釈文にしておいてください。
全体リスト構造解析を表示させるSubプロシージャhyoujirlstとhyouji1を作り、
hyoujirlstは下図の赤い場所に該当セルの候補数字を表示させること
hyouji1は解答に候補数字数を表示させること
をそれぞれ担当させてください。