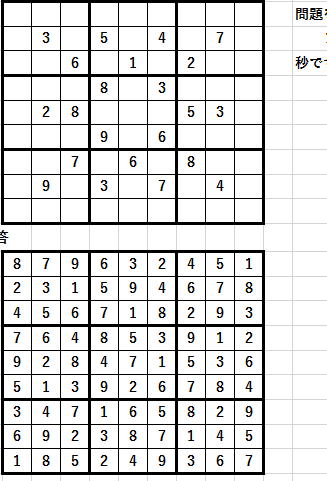
を実現するプログラム例
Dim n As Byte, m(8, 8) As Byte, cn As Integer, hnt As Byte 'nは数独の一辺、x(15)は数独を収納する配列、cnは数独総数をカウント、hntはヒント数
Dim iz(80) As Byte, jz(80) As Byte 'iz(80)はy座標を収納する配列、jz(80)はx座標を収納する配列
Dim cm(8, 8) As Byte 'm(i, j)のバックアップ
Private Sub CommandButton1_Click()
CommandButton2_Click
n = 9
Randomize (Timer) 'シード値を時間から取得
hj = Timer 'はじめの時間取得
Randomize (Timer) 'シード値を時間から取得
dainyu 'シートのB4からJ12のセルからm(i, j)に代入することが任務
f (0) '数独解答作成プロシージ
ow = Timer '終わりの時間取得
hyouji '解答表示
Cells(4, 12) = "問題を解くのにかかった時間は"
Cells(5, 12) = ow - hj
Cells(6, 12) = "秒です。"
End Sub
Sub dainyu() 'シートのB4からJ12のセルからm(i, j)に代入することが任務
Dim i As Byte, j As Byte, w As Byte
hnt = 0
w = 0
For i = 0 To n - 1
For j = 0 To n - 1
If Cells(4 + i, 2 + j) > 0 Then
m(i, j) = Cells(4 + i, 2 + j)
hnt = hnt + 1 'ヒント数のカウント
Else
m(i, j) = 0
iz(w) = i '入力順を確定させるためのy座標作成
jz(w) = j '入力順を確定させるためのx座標作成
w = w + 1
End If
Next
Next
cn = 0
End Sub
Sub f(g As Byte)
Dim i As Byte, j As Byte, k As Byte, h As Byte, w As Byte
Dim y As Byte, x As Byte, yy As Byte, xx As Byte
y = iz(g)
x = jz(g)
For i = 0 To n - 1
m(y, x) = i + 1
h = 1
For j = 0 To n - 1
If j <> x Then '行の座標(y, x)以外のすべてのセルについて重複検査をして、重複している場合にはhを0として以下の処理を実行させない。
If m(y, x) = m(y, j) Then
h = 0
Exit For
End If
End If
Next
If h = 1 Then
For j = 0 To n - 1
If j <> y Then '列の座標(y, x)以外のすべてのセルについて重複検査をして、重複している場合にはhを0として以下の処理を実行させない。
If m(y, x) = m(j, x) Then
h = 0
Exit For
End If
End If
Next
End If
If h = 1 Then
For j = 0 To n - 1
xx = 3 * Int(x / 3) + (j Mod 3)
yy = 3 * Int(y / 3) + Int(j / 3)
If x <> xx Or y <> yy Then 'ブロックの座標(y, x)以外のすべてのセルについて重複検査をして、重複している場合にはhを0として以下の処理を実行させない。
If m(y, x) = m(yy, xx) Then
h = 0
Exit For
End If
End If
Next
End If
If h = 1 Then
If g + 1 < n * n - hnt Then '行・列・ブロックの重複がなく、g + 1がn * n以下のときに、次のセル番号の世界に飛ぶ
f (g + 1)
If cn = 2 Then Exit Sub 'cn = 2となっている理由は別解がないか探索させるため
Else
cn = cn + 1 '数独総数カウント
If cn = 1 Then '別解がないか探索させている間にm(i ,j)は壊されてしまうためにバックアップをとっている。
For j = 0 To n - 1
For k = 0 To n - 1
cm(j, k) = m(j, k)
Next
Next
End If
If cn = 2 Then Exit Sub 'cn = 2となっている理由は別解がないか探索させるため
End If
End If
Next
m(y, x) = 0
End Sub
Sub hyouji()
Dim i As Byte, j As Byte
For i = 0 To n - 1
For j = 0 To n - 1
If cm(i, j) > 0 Then Cells(14 + i, 2 + j) = cm(i, j)
Next
Next
End Sub
Sub hyouji1()
Dim i As Byte
For i = 0 To n * n - hnt - 1
Cells(14 + iz(i), 2 + jz(i)) = i
Next
End Sub
Private Sub CommandButton2_Click()
Rows("14:22").Select
Selection.ClearContents
Range("L4:L11").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
隠していた時間は、

です。
3.79296875÷0.000083=約46000倍
もかかっています。
ヒント数0の疑似数独を解くより、
ヒント数22の数独を解く方が遙かに難しいのです。
約12万倍の時間を要したことを第1話で驚愕の結果と述べたのです。
数独を解くのに約4秒もかかったのでは、
もちろん数独自動出題ソフトは夢のまた夢です。
自分で問題を作成して解くという試行錯誤を
場合によっては数百回も繰り返さなければなりませんので、
お話になりません。
200回の試行錯誤で
ⅱ.解が存在する
ⅲ.別解が存在しない
を満たす数独が見つかったとすると、1題当たり
3.8×200=760秒=約12.7分
もかかってしまうのです。
幸運にも20回程度の試行錯誤で正しい数独を見つけたとしても1.27分程度です。
これでは開発に成功したとしても使ってくれるユーザはいませんね。
最悪でも1以内で生成できること、
出来れば数秒以内で出来ることが、
ユーザに使ってもらえるための条件と言えるでしょう。
ナンプレ自動生成アプリの絶対条件でしょう。
でもがっかりする必要はありません。
今回のソフトは疑似数独自動生成を直接に応用しただけで、
ほんの少しも工夫をしていないからです。
改良を重ねていくと、0.24秒程度でも解けるようになります。
つまり、15倍速化します。
それでも実用性がないとお考えかもしれませんが、
実は、今回の
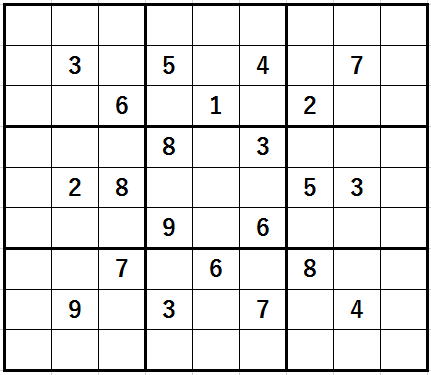
は数独解法ソフトにとってはかなり酷な問題なのです。
激辛数独12の問題でさえこれと同様な時間がかかる問題は1,2題というところで、
基本的には改良前でも3,4秒で解けてしまいます。
改良したソフトなら激辛数独は数題を除き0.1秒以下ですし、
問題によっては0.01秒程度で解けてしまいます。
激辛数独といえば難問中の難問です。
それが基本0.01秒から0.1秒程度で解けるなら、
数独自動作成アプリの解法エンジンとしては充分な能力を有していると言えるでしょう。
では、改良にとりかかっていきます。
次次話では、セルリスト構造解析と全体リスト構造解析・部分構造リスト解析を導入します。
全セルについてセルリスト構造解析をすることを全体リスト構造解析と呼び、
問題を解く過程でセルに入力したことによって影響を受けるセルのみに分析を限定するのを部分リスト構造解析と定義しています。
そして、セルリスト構造解析とは、そのセルに入る候補数字をすべてリストすることを表しています。
セルリスト構造解析・全体リスト構造解析・部分構造リスト解析があれば、
h = 1
For j = 0 To n - 1
If j <> x Then
If m(y, x) = m(y, j) Then
h = 0
Exit For
End If
End If
Next
If h = 1 Then
For j = 0 To n - 1
If j <> y Then
If m(y, x) = m(j, x) Then
h = 0
Exit For
End If
End If
Next
End If
If h = 1 Then
For j = 0 To n - 1
xx = 3 * Int(x / 3) + (j Mod 3)
yy = 3 * Int(y / 3) + Int(j / 3)
If x <> xx Or y <> yy Then
If m(y, x) = m(yy, xx) Then
h = 0
Exit For
End If
End If
Next
End If
の部分をすべて削除できますし、
If h = 1 Then
If g + 1 < n * n - hnt Then
f (g + 1)
If cn = 2 Then Exit Sub
Else
cn = cn + 1
If cn = 1 Then
For j = 0 To n - 1
For k = 0 To n - 1
cm(j, k) = m(j, k)
Next
Next
End If
If cn = 2 Then Exit Sub
End If
End If
は
If g + 1 < n * n - hnt Then
f (g + 1)
If cn = 2 Then Exit Sub
Else
cn = cn + 1
If cn = 1 Then
For j = 0 To n - 1
For k = 0 To n - 1
cm(j, k) = m(j, k)
Next
Next
End If
If cn = 2 Then Exit Sub
End If
とすることが出来ます。
注意深い読者なら気がついていますよね。
次次話 となっていたことに。
実は、改良に入る前に作った解答が正しいかどうか検証してほしいのです。
 検証は
検証は①解答に空欄がないこと、
問題に入っている数字と解答の同位置の数字が一致していること、
すなわち、②問題の数字が勝手に変更されていないこと、
③行にも列にもブロックにも数字の重複がないことの3点を調べて、
問題ないときは、「正しい解答です」と表示、
問題あるときは「正しくない解答です」と表示させてほしいのです。
もちろん、今回開発したソフトは徹底的に検証ツールで検証してありますので、
何万題解かせても間違えることはないでしょうが、
開発の歴史の中で、
完成したつもりでも1万題に1題程度複数解を持つ問題を出したり、
数万題に1題の割合で解のない問題を生成したりする不具合に遭遇したことがあります。
二百題に1題の割合で、
別解のある問題を生成してしまうという欠陥を発見したときには原因がわからず、
1週間も試行錯誤を繰り返した後に、
たった一カ所のタイピングミスを発見したこともあります。
普通はタイピングミスしたときには実行時にエラーしてしまうものですが、
そのときはたまたま動いてしまい、
原因の解明が困難になりました。
というわけで、100題程度の検証では不十分なのです。
数万題も検証するとなると、検証も自動化しておかなければならないのです。
ですから、検証ツールの開発は絶対に欠かすことが出来ないのです。
