第３講 試行錯誤法でヒント数０数独の解答を作る（２）
第７話 乱数を入れて自然＝不規則な配置にする

を実現するプログラム例

DDim n As Byte, m(8, 8) As Byte, cn As Integer 'nは数独の一辺、x(15)は数独を収納する配列、cnは数独総数をカウントする変数
Private Sub CommandButton1_Click()
　　CommandButton2_Click
　　n = 9 '縦横を9にしている
　　cn = 0
　　Randomize (Timer) 'シード値を時間から取得
　　f (0) '数独作成プロシージャ
End Sub
Sub f(g As Byte)
　　Dim i As Byte, j As Byte, h As Byte, a As Integer, s As Integer, w As Byte
　　Dim y As Byte, x As Byte, yy As Byte, xx As Byte, ii As Byte, iii As Byte
　　y = Int(g / n)
　　x = g Mod n
　　a = cn Mod 10
　　s = Int(cn / 10)
　　ii = Int(n * Rnd)
　　For i = 0 To n - 1
　　　　iii = (i + ii) Mod n
　　　　m(y, x) = iii + 1 '1から9までの数字を代入
　　　　h = 1
　　　　If x > 0 Then '行の重複を検査して、重複がある場合にはhを0として以下の処理をさせない。
　　　　　　For j = 0 To x - 1
　　　　　　　　If m(y, x) = m(y, j) Then
　　　　　　　　　　h = 0
　　　　　　　　　　Exit For
　　　　　　　　End If
　　　　　　Next
　　　　End If
　　　　If y > 0 Then '行の重複を検査して、重複がある場合にはhを0として以下の処理をさせない。
　　　　　　For j = 0 To y - 1
　　　　　　　　If m(y, x) = m(j, x) Then
　　　　　　　　　　h = 0
　　　　　　　　　　Exit For
　　　　　　　　End If
　　　　　　Next
　　　　End If
　　　　If h = 1 And y > 0 Then 'ブロックの重複を検査して、重複がある場合にはhを0として以下の処理をさせない。
　　　　　　For j = 0 To n - 1
　　　　　　　　xx = 3 * Int(x / 3) + (j Mod 3)
　　　　　　　　yy = 3 * Int(y / 3) + Int(j / 3)
　　　　　　　　If x = xx And y = yy Then Exit For
　　　　　　　　If x <> xx And y <> yy Then
　　　　　　　　　　If m(yy, xx) = m(y, x) Then
　　　　　　　　　　　　h = 0
　　　　　　　　　　　　Exit For
　　　　　　　　　　End If
　　　　　　　　End If
　　　　　　Next
　　　　End If
　　　　If h = 1 Then
　　　　　　If g + 1 < n * n Then '行・列・ブロックの重複がなく、g + 1がn * n以下のときに、次のセル番号の世界に飛ぶ
　　　　　　　　f (g + 1)
　　　　　　　　If cn = 10 Then Exit Sub '数独が10個生成した段階で探索をやめさせている。
　　　　　　Else
　　　　　　　　For j = 0 To n * n - 1 '数独が出来たのでシートに表示させている。
　　　　　　　　　　Cells(4 + Int(j / n) + (n + 1) * s, 2 + (j Mod n) + (n + 1) * a) = m(Int(j / n), (j Mod n))
　　　　　　　　Next
　　　　　　　　cn = cn + 1 '数独総数カウント
　　　　　　　　If cn = 10 Then Exit Sub '数独が10個生成した段階で探索をやめさせている。
　　　　　　End If
　　　　End If
　　Next
End Sub
Private Sub CommandButton2_Click()
　　Rows("4:30000").Select
　　Selection.ClearContents
　　Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル

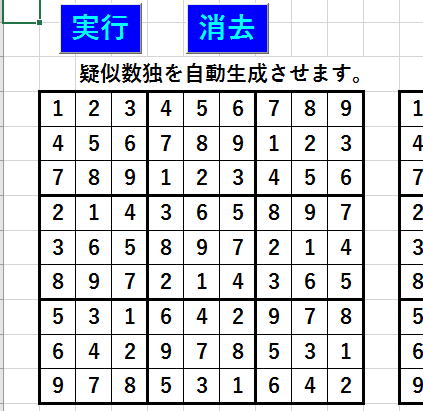
実は、ランダムを入れたことによって、

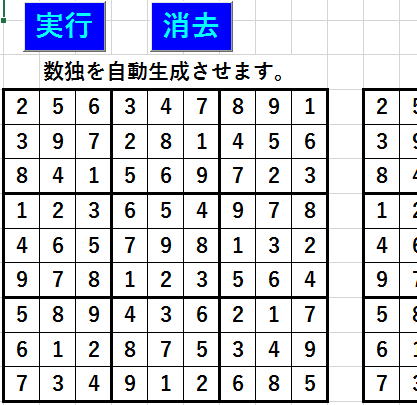
のように配置が自然＝不規則になり、
ここから問題を作れる可能が著しく増大しました。
本当は第６話で触れるべきでしたが、
自然＝不規則に対して違和感を覚える方はたくさんいらっしゃるのではないでしょう。
ですが、自然の法則は構造のあるもの＝規則のあるものは壊れていくというというものです。
秩序あるものは、秩序のないものへ、
熱が不均衡である場合均衡へ進んでいくのです。
コップの中のお茶は時間共に冷えていき、
最終的には室温と同じになります。
秩序が壊れていく、構造物が壊れていく、規則性が壊れていくことを、
エントロピー増大の法則というのです。
現代科学において解けていない難問があります。
秩序・構造・規則性が壊れていくのが自然の本来の姿なのに、
それに逆行している流れがあります。
なんだかわかりますか。
生物進化です。
生物はエントロピー増大の法則に反して、
構造をより複雑なものに変えてきています。
このアポリアを打開できたら現代科学の最も難解な問題を解いたことになります。
生物進化は謎であるにしても、
自然も社会も基本的には、秩序から無秩序へ、規則性のあるものから無規則性へ、
構造のあるものから平坦なものへ、
という運動法則を持っています。
ですが、社会はより複雑な政治制度や経済構造などを持つものに変化してきたのではないか、
という意見もあるでしょう。
トランプは北朝鮮で小型核を使うと明言しています。
小型核であっても核であるに違いありません。
アメリカが打てば北朝鮮やロシア・中国は核を打ち返すでしょう。
そうすると、止めどのない報復合戦になります。
結局人間は滅んでエントロピー増大の法則に従うしかないのかもしれませんよ。
本当のことをいうと私も書いていてわからなくなりました。
人間の歴史も生物進化と同じでエントロピーが減少しているのでしょうか。
それはおいておくとして、私は人類が核戦争で滅ばないようにするには、
憲法第９条を守り抜いて、世界に輸出していくしかないと思っています。
９条規定と同様な規定を持つ国は日本以外に２つありますが、
いずれの国も政治的にも経済的にも小国です。
経済大国である日本が９条規定を持っていることは大きな意味があると思っています。
平和を作り出すために必要なことは軍備を増強させることではありません。
軍拡は相互不信を醸成していくだけです。
平和の絶対的条件は、相互信頼の構築です。
これ以外に方法はありません。
ですから、第９条が果たした役割は無限大と言えるほど大きいのです。
政府が正式には侵略の事実を認めていないにもかかわらず、
第９条の存在が東南アジアやオーストラリア・ニュージーランドなどに大きな安心感を与えてきました。
第９条は外交文書なのです。
９条の存在は、私たちはアジアを侵略する意図はないことを明確に示すものだったのです。
ごめんなさい。
脱線が長くなりすぎましたね。



乱数を入れることにより
生成速度はどうなったでしょうか。

と同じように１万個の生成時間を調べるソフトを作って時間比較すなわち作成スピード比較をしてください。

トップへ