第7話 ハート型
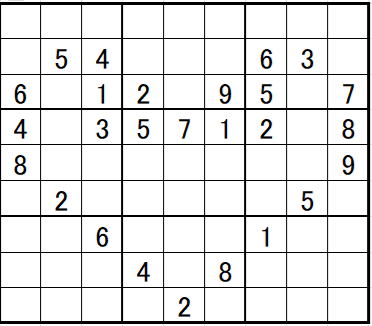

を実現するプロジェクト例
問題を解消することができました。
ヒント数26,27,28,29について5回ずつ実験しましたが、
ことごとくヒント数と入っている数字の個数が一致しました。
char main() {
・
・
・
hyg(A);
hys(A);
char k = 0;
for (unsigned char i = 0; i < n; i++) {
for (unsigned char j = 0; j < n; j++) {
if (gensudoku[A][i][j] > 0)k++;
}
}
cout << "数字が入っているものをカウント"<< + k << endl;
cout << "ヒント数"<< + hnt << endl;
・
・
・
if (s == n * n - 1) { //一番奥に部屋に到達
int k = rand() % 6;
if (k == 0)hitaisyou(a);
if (k == 1)sayutaisyou(a);
if (k == 2)jyogetaisyou(a);
if (k == 3)tentaisyou(a);
if (k == 4)sayujyogetaisyou(a);
if (k == 5)kokoro(a);
cn[a]++;
if (cn[a] == 1)return; //数独が1個できた時点でとめる
}
tobi:;
}
}
・
・
・
void kokoro(char a) {//ハート型
int k = hnt;
for (char i = 4; i < 9; i++) {
mondai[a][i][i - 4] = sudoku[a][i][i - 4];
gensudoku[a][i][i - 4] = sudoku[a][i][i - 4];
k--;
if (i < 8) {
mondai[a][i][12 - i] = sudoku[a][i][12 - i];
gensudoku[a][i][12 - i] = sudoku[a][i][12 - i];
k--;
}
}
for (char i = 2; i < 4; i++) {
mondai[a][i][0] = sudoku[a][i][0];
gensudoku[a][i][0] = sudoku[a][i][0];
k--;
mondai[a][i][8] = sudoku[a][i][8];
gensudoku[a][i][8] = sudoku[a][i][8];
k--;
}
mondai[a][2][2] = sudoku[a][2][2];
gensudoku[a][2][2] = sudoku[a][2][2];
k--;
mondai[a][2][6] = sudoku[a][2][6];
gensudoku[a][2][6] = sudoku[a][2][6];
k--;
mondai[a][1][1] = sudoku[a][1][1];
gensudoku[a][1][1] = sudoku[a][1][1];
k--;
mondai[a][1][7] = sudoku[a][1][7];
gensudoku[a][1][7] = sudoku[a][1][7];
k--;
mondai[a][2][3] = sudoku[a][2][3];
gensudoku[a][2][3] = sudoku[a][2][3];
k--;
mondai[a][3][4] = sudoku[a][3][4];
gensudoku[a][3][4] = sudoku[a][3][4];
k--;
mondai[a][2][5] = sudoku[a][2][5];
gensudoku[a][2][5] = sudoku[a][2][5];
k--;
//cout << "k = " << k << endl;
if (k % 2 == 1) {
int s = rand() % 4 + 4;
mondai[a][s][4] = sudoku[a][s][4];
gensudoku[a][s][4] = sudoku[a][s][4];
k--;
if (k == 0)return;
}
char p[11] = { 19,28,37,20,29,38,47,30,39,48,57 };
//
 青から1つ選び、緑からいくつか選んでその対称の場所も選び
青から1つ選び、緑からいくつか選んでその対称の場所も選び//ヒント数になるようにする。オレンジが20個なので、緑から2個選び青から1個選ぶと
//ヒント数は20 + 1 + 2×2 = 25となる。ヒント数が奇数の場合には青から奇数個選ばなければならない
//ホームページビルダーとエクセルでは色合いが異なるので完全に同じ色にはならないが、
//色対応に注意!2は左右対称性から
char t = 0;
char krk[11];
while (1) {
int h = 1;
while (1) {
krk[t] = rand() % 11;
if (t == 0)break;
for (char j = 0; j < t; j++) {
if (krk[t] == krk[j]) {
break;
h = 0;
}
if (h == 0)break;
}
if (h == 1)break;
}
char y = p[krk[t]] / 9;
char x = p[krk[t]] % 9;
mondai[a][y][x] = sudoku[a][y][x];
mondai[a][y][8 - x] = sudoku[a][y][8 - x];
gensudoku[a][y][x] = sudoku[a][y][x];
gensudoku[a][y][8 - x] = sudoku[a][y][8 - x];
k -= 2;
if (k == 0) return;
t++;
}
}
テキストファイル
テキストファイルは380行から
if (s == n * n - 1) { //一番奥に部屋に到達
int k = rand() % 5 + 1;
k = 5;
if (k == 0)hitaisyou(a);
if (k == 1)sayutaisyou(a);
if (k == 2)jyogetaisyou(a);
if (k == 3)tentaisyou(a);
if (k == 4)sayujyogetaisyou(a);
if (k == 5)kokoro(a);
cn[a]++;
if (cn[a] == 1)return; //数独が1個できた時点でとめる
}
となっていますが、ハート型がうまくいっているかを調べるためです。
ハート型うまくいっていることを確認できましたら
if (s == n * n - 1) { //一番奥に部屋に到達
int k = rand() % 5 + 1;
if (k == 0)hitaisyou(a);
if (k == 1)sayutaisyou(a);
if (k == 2)jyogetaisyou(a);
if (k == 3)tentaisyou(a);
if (k == 4)sayujyogetaisyou(a);
if (k == 5)kokoro(a);
cn[a]++;
if (cn[a] == 1)return; //数独が1個できた時点でとめる
}
と戻してください。
int k = rand() % 5 + 1;
は非対称を対象から外すためです。
非対称も対象に入れたい場合には、
int k = rand() % 6;
にすればよいのです。
次話でソフト作りをして『前半:解答から問題を作る』を終了したいと思います。
『後半:問題から解答を作る』においては、
理詰め解法エンジンを開発してVBAの支援を必要としないソフトを完成させます。
ヒントとなる数字を配置していく過程で 局所解析 = 単セル解析 = 空欄候補数字探索を
やっていきますので、当然行・列・ブロックでの数字の重複は生じません。
当然のことながら、前半で作ったものよりかなりの高速化が期待できます。
今回学んだことを活かして、数独自動生成ソフトを題材とするプログラミング知識0からの
C++入門またはVisual Sudio 2022 C++入門の講義を再開します。
このサイトの他の講義をのぞけばわかりますが、
トレースを私は重要視しています。
さて、後半に入る前にもう4つほど付け加えることをお許しください。
おそらく現行で左右対称・上下対称・点対称・左右にも上下にも対称・ハート型
ヒント数とコンソールに出力数えた数字の数は100%一致するもの思われましたが、
実験を続けていくと怪しいものもありました。
ハート型でしか実験していませんが、40回ほど実験してずれてしまう事例が残念ながら存在しました。
この程度 = 10回に1回程度なら、while文で成功するまで繰り返すプログラムも作り、
これなら完全にヒント数と実際の数は完璧に一致しましたが、
不完全なものには抵抗を感じます。
そこで、実際に配置してある数字の数とヒント数がずれてしまう原因を解明して第2案を作りました。
第2案は手動で各ヒント数で20回ほど実験した後に、下図の通り自動実験プログラムによって1000回以上実験し、
正しいことが確認されています。


第2案を提示する最大の理由は、後半のためにY座標とX座標を第1案に基づいて、
作ろうとしましたが複雑すぎて私には作れなかったことです。
第2案は最初からY座標とX座標を作っていますので、
コードはかなりわかりやすくなります。
対象に配置の話が途中ですが、
15話ぐらいになってしまいそうですから、
次話から第8講とさせていただきます。
第6話へ 第8講第1話へ
トップへ