第４話 Ⅰ.単セル解析（候補数字探索）で行った部分解析はなぜ逆部分解析を必要としないのか③
秘密は
void kyokusyokaiseki(int y, int x) {//局所解析 = 単セルリスト構造解析
for (int i = 0; i < n; i++)lst[y][x][i] = i + 1;//初期化{1,2,3,4,5,6,7,8,9}とする
mx[y][x] = 0;//{1,2,3,4,5,6,7,8,9}を{2,4}等にするために0に初期化 再カウントのため
for (int i = 0; i < n; i++) {//mondai[y][x]と同じ行にあるセルからの影響を調べる
if (i != x) {//自分自身は対象にしない
if (mondai[y][i] > 0) {
for (int j = 0; j < n; j++) {
if (lst[y][x][j] == mondai[y][i])lst[y][x][j] = 0;
//mondai[y][i]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (int i = 0; i < n; i++) {//mondai[y][x]と同じ列にあるセルからの影響を調べる
//2023年11月11に訂正 ごめんなさい。私の頭は主客転倒をしていました。
if (i != y) {
if (mondai[i][x] > 0) {
for (int j = 0; j < n; j++) {
if (lst[y][x][j] == mondai[i][x])lst[y][x][j] = 0;
//mondai[i][x]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (int i = 0; i < n; i++) {//mondai[y][x]と同じブロックにあるセルからの影響を調べる
if (3 * (y / 3) + (i / 3) != y && 3 * (x / 3) + (i % 3) != x) {
if (mondai[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)] > 0) {
for (int j = 0; j < n; j++) {
if (lst[y][x][j] == mondai[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)])lst[y][x][j] = 0;
//mondai[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)]と一致する数字を
//0にすることによって候補から外す
}
}
}
}
for (int i = 0; i < n; i++) {
if (lst[y][x][i] > 0) {
lst[y][x][mx[y][x]] = lst[y][x][i];//例えば、{0, 2, 0, 4, 0, 0, 0, 0, 0}を{ 2,4 }と詰めて0を含めない
mx[y][x]++;
}
}
}
局所解析にあります。
色のついている２行こそが回答（解答ではなくあえてこちらの漢字を使います）です。
for (int i = 0; i < n; i++)lst[y][x][i] = i + 1;//初期化{1,2,3,4,5,6,7,8,9}とする
mx[y][x] = 0;//{1,2,3,4,5,6,7,8,9}を{2,4}等にするために0に初期化 再カウントのため
の２行でやっていることは初期化です。
一度他のセルから受けた影響をリセット（すべてキャンセル）して、
再解析=再分析をしています。
候補数字を｛1，2，3，4，5，6，7，8，9｝に戻して再解析をやっているので、
部分解析のキャンセルがいらないのです。
逆部分構造解析が私の前に立ちはだかった最大の難問でした。
ですが、局所解析をすれば不要な門であることを発見したときには、
感激のあまり涙が出そうになりました。
--------------------------------------------------------------------------------------------
申し訳ございません。上の説明は間違いです。
第４講第９話のコード
if (i == mx[Y[g]][X[g]] - 1) {
//i < mx[Y[g]][X[g]] - 1)のときはiが１つ進んで上で単セル解析（候補数字探索）を行うので
//キャンセルは不要だが、最後だけはキャンセルをしなければならないので単セル解析（候補数字探索）
//を行う必要がある
の注釈文に書いてある通り、
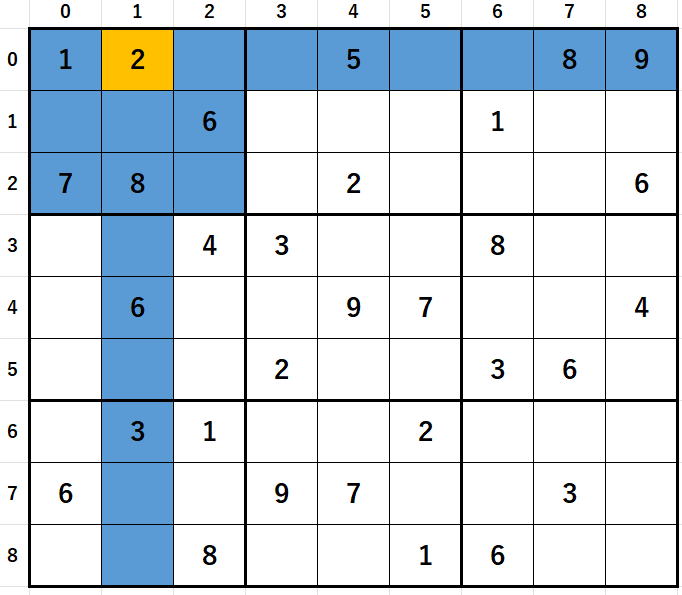
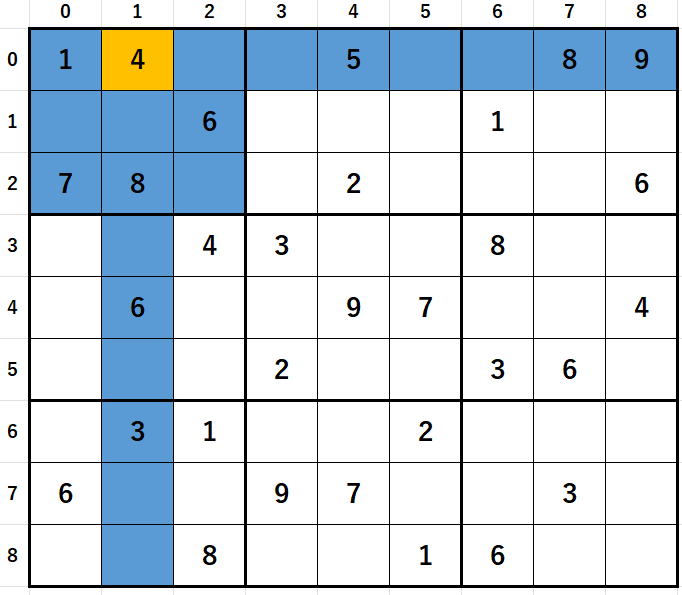
４の場合で部分解析をやり直しているので、
２の場合で行った部分解析のキャンセルは必要ないわけです。
４で部分解析をやり直す際に、
for (int i = 0; i < n; i++)lst[y][x][i] = i + 1;//初期化{1,2,3,4,5,6,7,8,9}とする
mx[y][x] = 0;//{1,2,3,4,5,6,7,8,9}を{2,4}等にするために0に初期化 再カウントのため
この２行が働いています。
全体構造解析によって候補は
｛2，4｝であることが確認されています。したがって、４の場合には候補数字が残されていませんので、
別の数字でやり直すことができないために
if (i == mx[Y[g]][X[g]] - 1) {
//i < mx[Y[g]][X[g]] - 1)のときはiが１つ進んで上で単セル解析（候補数字探索）を行うので
//キャンセルは不要だが、最後だけはキャンセルをしなければならないので単セル解析（候補数字探索）
//を行う必要がある
//cout << "*-*-*-*-復元-*-*-*-*-*" << endl;
mondai[Y[g]][X[g]] = 0;
//cout << g << endl;
for (int j = 0; j < n; j++)if (j != X[g])if (mondai[Y[g]][j] == 0)kyokusyokaiseki(Y[g], j);
for (int j = 0; j < n; j++)if (j != Y[g])if (mondai[j][X[g]] == 0)kyokusyokaiseki(j, X[g]);
for (int j = 0; j < n; j++) {
if (s + (j / 3) != Y[g] && t + (j % 3) != X[g]) {
if (mondai[s + (j / 3)][t + (j % 3)] == 0) {
kyokusyokaiseki(s + (j / 3), t + (j % 3));
}
}
}
}
によってキャンセルする必要があるわけです。
したがって、Ⅰ.単セル解析（候補数字探索）で行った部分解析はなぜ逆部分解析を必要としないのか
の問い方も間違いです。
皆様に混乱を与えたと思います。心よりお詫び申し上げます。
すべて削除してやり直すべきかもしれませんが、
思考過程を残しておくことは参考になると考えて間違った記述をあえて残します。
どうかお許しください。
--------------------------------------------------------------------------------------------
他のセルの放射線によって影響をうけた候補数字を
for (int i = 0; i < n; i++) {//mondai[y][x]と同じ行にあるセルへの影響を調べる
if (i != x) {//自分自身は対象にしない
if (mondai[y][i] > 0) {
for (int j = 0; j < n; j++) {
if (lst[y][x][j] == mondai[y][i])lst[y][x][j] = 0;
//mondai[y][i]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (int i = 0; i < n; i++) {//mondai[y][x]と同じ列にあるセルへの影響を調べる
if (i != y) {
if (mondai[i][x] > 0) {
for (int j = 0; j < n; j++) {
if (lst[y][x][j] == mondai[i][x])lst[y][x][j] = 0;
//mondai[i][x]と一致する数字を0にすることによって候補から外す
}
}
}
}
for (int i = 0; i < n; i++) {//mondai[y][x]と同じブロックにあるセルへの影響を調べる
if (3 * (y / 3) + (i / 3) != y && 3 * (x / 3) + (i % 3) != x) {
if (mondai[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)] > 0) {
for (int j = 0; j < n; j++) {
if (lst[y][x][j] == mondai[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)])lst[y][x][j] = 0;
//mondai[3 * (y / 3) + (i / 3)][3 * (x / 3) + (i % 3)]と一致する数字を
//0にすることによって候補から外す
}
}
}
}
によって 0 として外します。
そして、
for (int i = 0; i < n; i++) {
if (lst[y][x][i] > 0) {
lst[y][x][mx[y][x]] = lst[y][x][i];//例えば、{0, 2, 0, 4, 0, 0, 0, 0, 0}を{2, 4}と詰めて0を含めない
mx[y][x]++;
}
}
で 0 を詰めて再登録しているのです。
これで謎の１つ（なぜ逆部分構造解析をしなくてもよいのか）は解かれました。
でも第５講第１話で述べた『時』や第４講第８話で触れた『主客転倒』などの意味ありげな言葉については、
まだ何も語られていませんので第７話辺りで詳しく説明します。
具体例を出して流れを追ってみましょう。
（そんなのわかっているよと思う方は第８話に進んでください）
コンピュータの動きを追うことをトレースといいます。
トレースを読むときには色対応に注意しながら読んでください。
y = 0, x = 2のとき
for (int i = 0; i < n; i++) {//mondai[y][x]と同じ行にあるセルからの影響を調べる
if (i != x) {//自分自身は対象にしない
if (mondai[y][i] > 0) {
for (int j = 0; j < n; j++) {
if (lst[y][x][j] == mondai[y][i])lst[y][x][j] = 0;
//mondai[y][i]と一致する数字を0にすることによって候補から外す
}
}
}
}
{1,2,3,4,5,6,7,8,9}を順番をカウントするとき（0 + 1)番目，（1 + 1)番目，（2 + 1)番目，（3 + 1)番目，（4 + 1)番目，
（5 + 1)番目，（6 + 1)番目，（7 + 1)番目，（8 + 1)番目であることに注意！
プログラミングは基本は0から数え始めるため
ｉ = 0 のとき （y = 0, x = 2）が前提
if (0 != 2) {//自分自身は解析対象にしない
if (mondai[0][0] > 0) {
の２条件は満たされ
for (int j = 0; j < n; j++) {
if (lst[0][2][j] == mondai[0][0])lst[0][2][j] = 0;
//mondai[y][i]と一致する数字を0にすることによって候補から外す
}
が実行されます。
j = 0のとき （初期化されているので（y = 0, x = 2）の数字候補は{1,2,3,4,5,6,7,8,9}
if (lst[0][2][0] == mondai[0][0])lst[0][2][0] = 0;
if (1 == 1)lst[0][2][0] = 0;
//1は{1,2,3,4,5,6,7,8,9}の（0 + 1）番目 1は
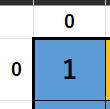座標(0, 0)の11 == 1は成り立ちlst[0][2][0] = 0;が実行され{0,2,3,4,5,6,7,8,9} 1が候補から外された！
j = 1のとき （（y = 0, x = 2）の数字候補は{0,2,3,4,5,6,7,8,9}
if (lst[0][2][1] == mondai[0][0])lst[0][2][1] = 0;
if (2 == 1)lst[0][2][1] = 0;
//2は{1,2,3,4,5,6,7,8,9}の（1 + 1）番目 1は
座標(0, 0)の12 == 1は正しくないので何もされずに{0,2,3,4,5,6,7,8,9}
j = 2のとき （（y = 0, x = 2）の数字候補は{0,2,3,4,5,6,7,8,9}
if (lst[0][2][2] == mondai[0][0])lst[0][2][2] = 0;
if (3 == 1)lst[0][2][2] = 0;
//3は{1,2,3,4,5,6,7,8,9}の（2 + 1）番目 1は
座標(0, 0)の13 == 1は正しくないので何もされずに{0,2,3,4,5,6,7,8,9}
j = 3のとき （（y = 0, x = 2）の数字候補は{0,2,3,4,5,6,7,8,9}
if (lst[0][2][3] == mondai[0][0])lst[0][2][3] = 0;
if (4 == 1)lst[0][2][3] = 0;
//4は{0,2,3,4,5,6,7,8,9}の（3 + 1）番目 1は
座標(0, 0)のセルの内容の14 == 1は正しくないので何もされずに{0,2,3,4,5,6,7,8,9}
j = 4のとき （（y = 0, x = 2）の数字候補は{0,2,3,4,5,6,7,8,9}
if (lst[0][2][4] == mondai[0][0])lst[0][2][4] = 0;
if (5 == 1)lst[0][2][4] = 0;
//5は{0,2,3,4,5,6,7,8,9}の（4 + 1）番目 1は
座標(0, 0)のセルの内容の15 == 1は正しくないので何もされずに{0,2,3,4,5,6,7,8,9}
j = 5のとき （（y = 0, x = 2）の数字候補は{0,2,3,4,5,6,7,8,9}
if (lst[0][2][5] == mondai[0][0])lst[0][2][5] = 0;
if (6 == 1)lst[0][2][5] = 0;
//6は{0,2,3,4,5,6,7,8,9}の（5 + 1）番目 1は
座標(0, 0)のセルの内容の16 == 1は正しくないので何もされずに{0,2,3,4,5,6,7,8,9}
j = 6のとき （（y = 0, x = 2）の数字候補は{0,2,3,4,5,6,7,8,9}
if (lst[0][2][6] == mondai[0][0])lst[0][2][6] = 0;
if (7 == 1)lst[0][2][2] = 0;
//7は{0,2,3,4,5,6,7,8,9}の（6 + 1）番目 1は
座標(0, 0)のセルの内容の17 == 1は正しくないので何もされずに{0,2,3,4,5,6,7,8,9}
座標(