0から80という81個の数字ですから難しくなります。
そこで数字の種類を減らして
1 2 3 4 5
出発点を選びそこからいくつ飛びで考えます。
ただし、右がない場合には一番左に戻ります。
出発視点を3で飛びを2として変化を負います。
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
5回で網羅されました。次は4からスタートして3飛びをやってみます。
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
ここまでくると5個の数字の場合には出発地点と飛びをいかように選んでも、
5回でも網羅されるという結論が出そうです。
怪しいと思う方はその他もやってみてください。
1 2 3 4 5 6
でやってみましょう。スタート地点2、飛び3とすると、
1 2 3 4 5 6
1 2 3 4 5 6
1 2 3 4 5 6
1 2 3 4 5 6
1 2 3 4 5 6
1 2 3 4 5 6
永久ループです。
1 2 3 4 5 6
1 2 3 4 5 6
1 2 3 4 5 6
永久ループです。
もちろん、飛びを1つとすれば0から80であっても81回で網羅することができますが、
この場合例えばヒント数20のとき、
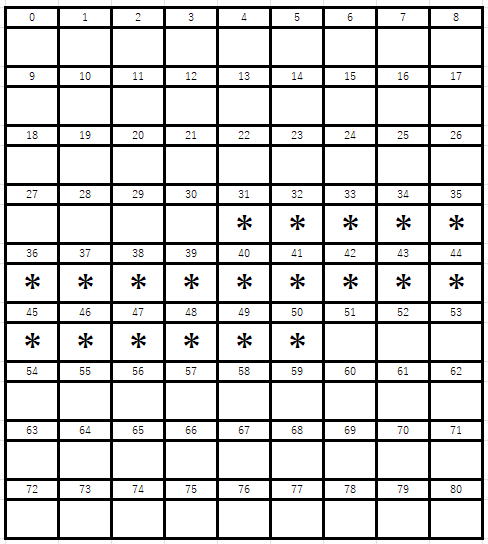
となってしまいます。始めの位置は31です。
31からかためてヒントになる数が配置されていて、
数独が成立することはあり得ません。

このように自然な配置でないと数独は成立しません(対称性はのちの課題となります。)
ですから、解かなければならない問題なのです。
あなたはこの難問解けますか。
ヒントは互いに素です。
実は、今使ったエクセル(クリックすると入手できます)

となっています。コードは
Private Sub CommandButton1_Click()
CommandButton2_Click
Dim h As Integer, i As Integer, st As Integer, tb As Integer, hn As Integer
st = Cells(9, 15) 'スタート地点
tb = Cells(11, 15) '飛び
hn = Cells(7, 15) 'ヒント数
Dim a(81) As Integer
Dim y(80) As Integer, x(80) As Integer
For i = 0 To 80
Cells(2 + 2 * Int(i / 9), 2 + Int(i Mod 9)) = i
Next
For i = 0 To hn - 1
a(i) = (st + tb * i) Mod 81
Next
For i = 0 To hn - 1
Cells(3 + 2 * Int(a(i) / 9), 2 + a(i) Mod 9) = "*"
Next
End Sub
Private Sub CommandButton2_Click()
Range("B2:J23").Select
Selection.ClearContents
Range("A2").Select
End Sub
ところが、飛びを12などとしてしまうと

と不自然な配置となりもちろん数独は成立しません。
飛びはどのような数字を選べばよいのでしょうか。
第8話へ 第10話へ
トップへ