数独自動生成ソフト開発で学ぶ超初心者のためのC++マルチスレッドプログラミング入門　　
第１講　序章（周辺の説明とプログラミング体験）
第４話 　理詰めで解くはなんとなくわかったけど、もう少し具体的に説明すると？

その説明は、私がかつてワードで書いたナンプレの解き方を引用して次善の策とさせていただきます。

---------以下引用---------------------------------------------------------------------------

ナンプレの解き方（基礎編）

初心者の方は、最初に空欄に入る数字の候補を探しているのではないでしょうか。そして、比較的候補数が少ない空欄で、ある数を仮定して進めていき、矛盾するとその数字を捨てるという方法を使っていませんか。この方法を仮定法とか試行錯誤法と呼び、数独やナンプレのファンは邪道な方法と見なします。試行錯誤法を『ナンプレを解く方法』として認めるなら、コンピュータは激辛数独の一番難しい問題でさえ、0.01秒程度で解いてしまいます。

　私もナンプレファンの1人であり、仮定法を解法としては認めていません。すべての場合を調べ尽くせば、解答に至るのは当たり前の話です。どんなに難しい迷路でも実は必勝法があります。どちらかの壁を手で触って進んでいけば必ず出口に到達することが出来ます。試行錯誤法はそれと似たやり方であると思います。

　私の開発したソフトは仮定法を使わなければ解けない問題は１題たりとも生成しません。必ず理詰めで解ける問題のみを作り出します。空欄の中に最低でも１個は、1つの数字に確定できる欄が必ずあるのです。ですから、ナンプレの王道と言える解き方は、空欄の中の確定できる『ます』を探し出すことです。例え、空欄が64個あったとしても必ずどこかの『ます』は１つの数字に確定できるのです。そして、その数字を入れることによって再び少なくても１個の『ます』は1つの数字に確定できるようになるのです。ソフトは確定した数字を入れていく作業の連続によって必ず解ける問題しか出題しないのです。一般的には理詰めと呼ばれていますが、私は、１つに数字に確定した『ます』に入れていくので確定法と呼んでいます。一切仮定法をつかずに、確定法で解いたときの達成感は半端ではありません。ナンプレ自動生成アプリの開発者としては仮定法による解法を是非ともやっていだきたくないというのが願いです。なぜなら、仮定法を使わずに確定法で解いたときの喜びは次元が異なるからです。感動の次元が違うのです。

　では、1つの数字に確定できる空欄をどのように探し出すのでしょうか。コツはたったの６つしかありません。ライン排除・ライン間接排除・１：１対応確定による排除・リスト法（空欄に入る数字の候補を探し出す方法）・＃排除です。順番は、適当に書いたものではなく、この順に考えていくと最も効率的に解ける解法順なのです。『ます』に入る候補を探し出す作業は、ライン排除とライン間接排除によって可能な限り数字を埋めてからはじめて行うのが、ナンプレを早く解く方法なのです。しかも、空欄候補探索(リスト探索)は候補が３つ以下の時に限定されます。４個になってしまった時点で探索をやめ消しゴムで消します。理由は、候補が１個になっている『ます』を探すか、１：１対応確定による排除が出来るかどうかを調べるためにリスト探索を行うからです。それでは順にそれぞれのコツを説明していきましょう。

※以下空欄可能性探索とか、空欄探索などの言い回しが出てきますが、気分で言いかえているだけで、すべてリスト法（空欄に入る数字の候補を探し出す方法）のことです。解法はライン排除・ライン間接排除・１：１対応確定による排除・リスト法（空欄に入る数字の候補を探し出す方法）・＃排除の6つしかないです。

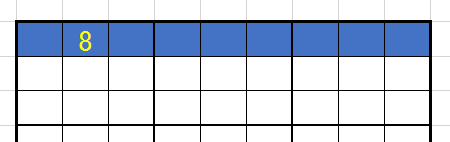
　まず、解法において最も重要であるライン排除から。中級以下の問題であれば、このライン排除法のみによってほとんど解けてしまいます。ライン排除とは、同じ行（横列）・同じ列（縦列）には、同じ数字を入れてはならないというナンプレのルールを視覚で表しただけものです。行や列上にある数字がそのラインにある空欄にその数字の入る可能性を排除するので、ライン排除と呼んでいるわけです。色のついている空欄には、８を入れることは出来ませんね。

　ライン排除を使うと下の図で１つの数字に確定できる空欄が存在しています。どれだかわかりますか。

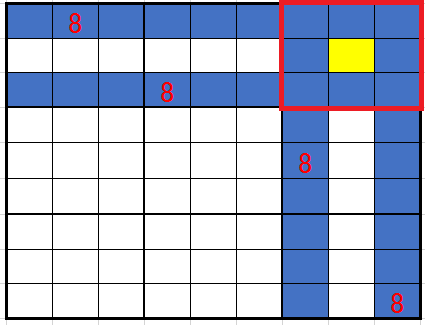
赤い四角で囲んだブロックに注目して下さい。８が入る可能性を否定されていない『ます』は１個しかないですね。そうです。黄色の『ます』です。空欄探索法なら１から９のすべてが可能ですが、ライン排除法は１つの数字に確定してしまうのです。視覚であらわしただけで破壊的な効果をもたらすのです。

次にブロック排除について説明しましょう。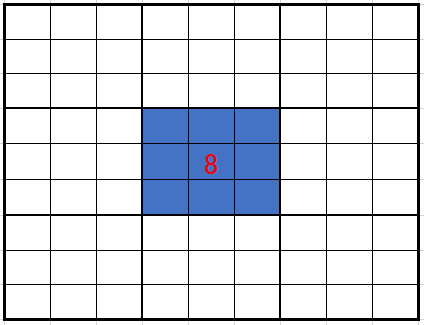

ブロック排除とはブロックの『ます』に入っている数字がそれ以外のブロックの『ます』にその数字が入る可能性を否定することを指します。ライン排除とブロック排除を組み合わせますと、

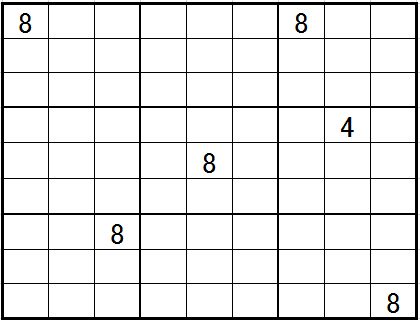
この図の中に確定できる『ます』があることがわかります。どこでしょうか。ヒントは

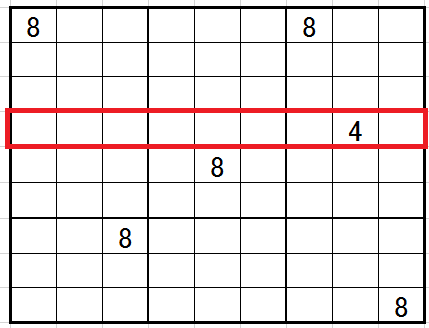
赤い囲いの行に注目することです。

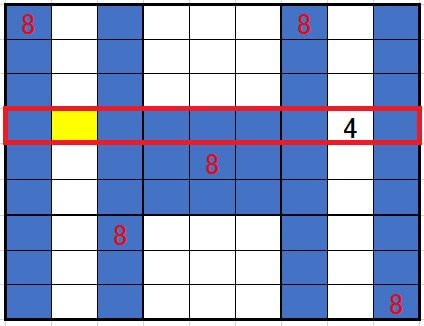
黄色い『ます』以外に８が入るところはありませんね。今回も空欄の可能性を探るだけなら、４以外のすべてが可能ですよね。初心者が陥りやすいリストを探る方法が、いかに非効率的な方法であるかを示していませんか。ただし、リスト法はなければならない方法であり、局面によっては数字を確定させる方法であるのです。

ライン間接排除の説明に移ります。私は、ライン反照排除と呼んでいましたが、今回からライン間接排除と名称を変更します。理由は、反射排除より広い概念であることがわかったからです。まず、ライン反照排除の事例から示しましょう。

　この事例の赤色のところには８は入りません。理由は、

８のライン排除によって,オレンジのいずれかに８が入ることが確定してその結果新たなライン排除が発生するからです。赤はその左の３つの空欄まで伸ばすことが出来ますが、もともと８のブロック排除によって排除されていますので、意味のある排除は赤のみとなります。反照とは反射のことです。反射して赤まで排除してしまうので反照排除としたわけです。

　当然、８は真ん中のブロックの白いところに入ることになります。ですから、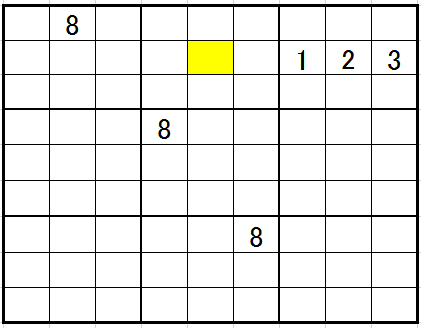

なら、黄色のところに８が入ることが確定します。ライン排除とライン反照排除を考えればよいですね。

　次に名称を間接と変更されざるを得なかった事例を載せます。

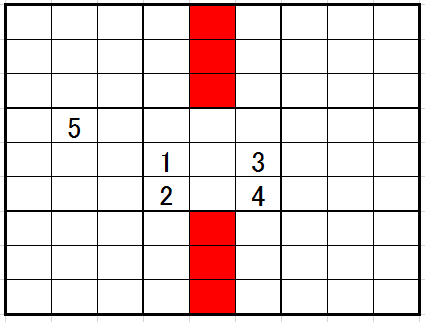
　赤は５の可能性が排除されます。理由は、

５のライン排除によってオレンジのいずれかに５が入ることが確定します。その結果新たなライン排除が発生して赤に５が入る可能性が排除されたからです。

　２つの事例は、ライン排除によって同じライン上に該当となる数字が入ることによって新にライン排除が発生していることが共通しています。なので、ライン間接排除の名称としたわけです。

　ではどんな場合に、このライン間接排除によって確定『ます』が生じるのでしょうか。

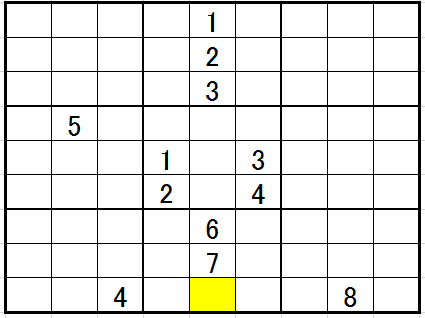
　黄色は９ですね。理由はおわかりですね。リスト法はこのような局面で用いるのです。

１：１対応確定による排除とは何でしょうか。一見数学的な概念に見えて、高度なことを言っているように見えるかもしれませんが、内容は究めて簡単なことです。そもそも、高校数学教諭であった者として、述べたいことは、数学の概念は究めて自明なことを主張しているだけで誰でも理解できる当然の真理しか主張していないのだと、と言うことです。　

１：１対応確定とは、空欄数と候補数が同じであるときには、その空欄にいずれかの数字が入ることが確定するという事実を指しています。例えば、

２つの空欄に３と４しかリストされないとすると、どちらかの欄には３と４が入ることが確定します。もし、３が入らないとすると、３の行き場がなくなってしまいますよね。４も同様です。このときに肝要なことは、３と４のライン排除

が発生するということです。例えば、

ならば、黄色の空欄が１に確定します。排除されている可能性は２，３，４，５，６，７，８，９であるからです。

でも同じです。

　２つの『ます』に２つの同じ数字のみが候補となるとき、いずれかの『ます』のその数字が入ることが確定して、その結果そのライン上にはその２つの数字が入らないことが確定することになることを２on２確定と排除と名付けます。あるいは、相補確定と排除と呼ぶことにします。相補確定とは、２つの数字がお互いに補い合って確定する自体を指しています。

　ではどのような場面で相補確定の原理が働くのでしょうか。

　オレンジに入る数字の候補を考えて下さい。２と７のみしかリストされませんね。この際に大事なことは、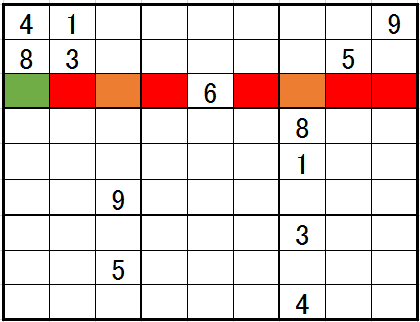

例えば、緑の候補は相補確定による排除を考えなければ、２，５，７，９

であるのに対して考えれば、

５，９

となることです。候補が減ることによって確定に近づいていくのです。赤いセルもすべて２，７がリストから外されます。

　同様に３つの空欄に同じ３つの数字のみがリストされる時を３on３と名付けます。

この場合にも確定と排除が発生します。

オレンジのいずれかに３と４と５が入ることが確定して、紺には３と４と５が入らないことが確定する訳です。つまり３on３確定と排除が発生します。

当然、なら

黄色に９が入ることが確定します。

の黄色も９しか入りません。

　３on３には、いくつかの変則バージョンが存在します。

などです。

　最後に＃排除について説明します。ニコリでは井形理論と呼んでいますが、私の名称の方が優れていると思います。理由は＃の形に排除するからです。では、どのような局面で＃排除は発生するのでしょうか。それは次のような局面です。

その局面とは、AまたはBに３（何の数字でも同じです。今は3で説明します。）が入り、同じくCまたはDに３が入るような場合です。この場合には、

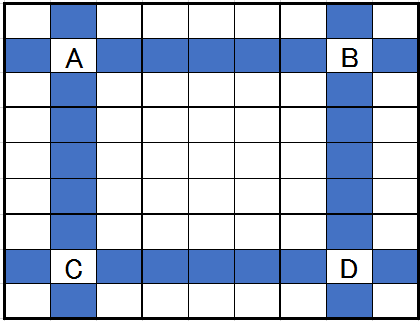
色のついているところには３の入る可能性が排除されます。＃形に排除されるので＃排除と呼んでいるわけです。どうしてだかわかりますか。

３は（AとD）に入るか、（BとC）に入るかの２つのケースしかありません。なぜなら、（AとB）または（CとD）に入ってしまえば、同じ行には同じ数字を入れることが出来ないというナンプレのルールを満たさないからです。（AとD）に入る場合にも、（BとC）に入る場合にもいずれにしても同じ行と列には同じ数字を入れることが出来ませんので＃上に排除が発生するのです。

　具体的にはどんな局面で＃排除が発生するのでしょうか。

３は（AまたはB）あるいは（CまたはD）にし入る可能性がありませんね。このような局面は、月刊誌の問題では発生しません。なぜなら、＃排除を使う問題は、超上級クラスであるからです。激辛数独12のような専門誌でしかお目にかかることはありません。しかも、ライン排除・ライン間接排除・１：１対応確定による排除を徹底的に行い、かなり数字を埋めた段階でしか、遭遇することはありません。

　尚、

（AまたはC）に3が入り、（BまたはD）に3が入る場合でも＃排除は発生します。理由は同じで、３が入るとしたら（AとD）か（CとB）のように対角線に入るしか考えられませんね。（AとC）または（BとD）なら同じ列に同じ数字３が入ってしまいますね。

　さて、基礎編は終わりにしまして、応用編へと移行します。応用編ではヒント数22程度のナンプレを解いていきます。

---------以上引用---------------------------------------------------------------------------
応用はまだ書いていませんので、応用編を読みたいと思っている方は多いと思いますが、後の課題ということでお許しください。


第３話へ　第５話へ

トップへ